Modul Thermodinamika Teknikpengabdian masyarakat

Modul Thermodinamika Teknik

MODUL

THERMODINAMIKA TEKNIK

DISUSUN OLEH :

Ir. Rudy Yulianto, MT

JURUSAN TEKNIK MESIN

FAKULTAS TEKNOLOGI INDUSTRI

UNIVERSITAS JAYABAYA

JAKARTA

DAFTAR ISI

BAB 1. Pendahuluan. 1

BAB 2. Sifat-sifat Gas Sempurna. 14

BAB 3. Proses Termodinamika Gas Sempurna. 26

BAB 4. Entropi Gas Sempurna. 43

BAB 5. Sifat-sifat Zat Murni. 59

BAB 6. Siklus Udara Termodinamika. 66

BAB I

PENDAHULUAN

1.1. Hukum Gerak

Newton telah merumuskan tiga hukum tentang gerak, dimana merupakan dasar asumsi untuk sebuah sistem dinamis. Ketiga hukum tentang gerak ini dikenal sebagai:

1. Hukum pertama Newton tentang gerak.

2. Hukum kedua Newton tentang gerak.

3. Hukum ketiga Newton tentang gerak.

1.1.1. Hukum Pertama Newton

Menyatakan : Setiap benda akan tetap diam atau bergerak secara teratur dalam sebuah garis lurus, kecuali ada gaya yang bekerja padanya.

1.1.2. Hukum Kedua Newton

menyatakan: Laju perubahan momentum secara langsung berbanding lurus dengan gaya yang bekerja dan terjadi pada arah yang sama dengan arah gaya yang bekerja.

Misalkan sebuah gaya bekerja pada sebuah benda yang membuat benda itu bergerak. Katakan:

m = massa benda

F = gaya yang bekerja

u = kecepatan awal benda

v = kecepatan akhir benda

t = waktu benda tersebut merubah kecepatannya dari u ke v dalam detik. Menurut hukum kedua Newton tentang gerak:

F ∝ mv − mu ∝ m(v − u )

t t

F ∝ ma - kma dimana a =percepatan= (v-u)/t

k adalah konstanta.

1.1.2.1. Massa dan Berat

a. Massa

Adalah jumlah materi yang terkandung pada suatu benda, dan tidak berubah karena perubahan posisinya di permukaan bumi. Massa benda diukur dengan perbandingan langsung dengan massa standar dengan menggunakan timbangan.

b. Berat

Adalah jumlah tarikan, dari bumi terhadap suatu benda. Karena besar tarikan berubah karena perbedaan jarak benda terhadap pusat bumi, maka berat benda juga akan berubah karena perubahan posisinya di permukaan bumi. Jadi jelas bahwa berat adalah sebuah gaya.

Besar tarikan bumi dalam satuan Metriks, pada level permukaan laut dan lintang

450, telah diambil sebagai satu satuan gaya dan disebut satu kilogram gaya. Sayangnya satuannya sama dengan satuan massa.

Berat benda diukur dengan menggunakan timbangan pegas, yang akan menunjukkan variasi tarikan pegas jika benda dipindahkan dari satu tempat ke tempat lain.

Pada satuan CGS, satuan gaya adalah dyne. Satu dyne didefinisikan sebagai gaya, ketika bekerja pada massa satu gram, akan menghasilkan percepatan sebesar 1 cm/sec2 pada arah gaya yang bekerja tersebut.

Demikian pula dalam satuan MKS atau SI, satuan gaya disebut Newton (disingkat N). Satu Newton didefinisikan sebagai gaya, ketika bekerja pada massa satu kilogram, akan menghasilkan percepatan 1 m/sec2 pada arah gaya yang bekerja tersebut.

1.1.2.2. Satuan Absolut dan Gravitasi dari Gaya

Dari penjelasan diatas, jika sebuah benda bergerak dengan percepatan 9,81 m/sec2, gaya yang bekerja pada benda tersebut adalah 9,81 N. Tetapi kita tahu bahwa massa 1 kg yang mengalami tarikan bumi dengan percepatan 9,81 m/sec2 adalah 1 kg-berat. Sehingga:

1 kg-berat = 9,81 N

dengan cara yang sama:

1 gm-berat = 981 dyne

Satuan gaya diatas yaitu kg-berat dan gm-berat (untuk kemudahan biasanya ditulis hanya kg dan gm) disebut gravitasi atau satuan ahli teknik tentang gaya, sedangkan Newton dan dyne disebut satuan absolut atau satuan saintific gaya.

Untuk membedakan satuan massa dengan berat, diperkenalkan massa benda dalam satuan yang baru yaitu Khurmi, dimana 1 Khurmi adalah massa benda dalam kg dibagi dengan percepatan gravitasi (g=9,81).

1.1.3. Hukum Newton Ketiga

Tentang Gerak

Menyatakan bahwa “setiap aksi, selalu ada reaksi yang sama besarnya dan berlawanan arah”.

1.1.3.1. Kerja

Jika sebuah gaya bekerja pada sebuah benda dan benda mengalami perpindahan, dikatakan bahwa telah dilakukan kerja. Contohnya, jika sebuah gaya F bekerja pada sebuah benda sehingga menghasilkan perpindahan x pada arah gaya, kemudian kerja yang dilakukan oleh gaya:

W = F . x

Satuan kerja bergantung pada satuan gaya dan perpindahan. Pada sistem MKS, satuan kerja adalah kilogram-meter (kg-m). Dalam sistem SI, satuan kerja adalah Newton- meter (N-m).

1.1.3.2. Daya

Adalah laju kerja atau kerja per satuan waktu. Daya adalah pengukuran kinerja suatu mesin, misalnya: sebuah mesin melakukan sejumlah kerja dalam satu detik akan dua kali lebih bertenaga dari pada mesin yang mengerjakan kerja yang sama dalam dua detik. Secara matematik Daya:

Daya = Kerja yang dilakukan

Waktu yang digunakan

Dalam sistem Metrik, satuan daya adalah daya kuda yang sama dengan 4500 kg-m per menit atau 75 kg-m per detik. Dalam sistem SI, satuan daya adalah Watt, yaitu sama

dengan 1 N-m/s atau 1 J/s. Umumnya satuan daya yang lebih besar digunakan kilowatt

(kW) yaitu sama dengan 1000 W.

1.1.3.3. Energi

Energi didefinisikan sebagai kapasitas untuk melakukan kerja. Energi dijumpai dalam berbagai bentuk, yaitu: mekanik, listrik, kimia, panas, cahaya dsb. Energi mekanik terdiri dari:

1. Energi potensial.

2. Energi kinetik.

Energi potensial dipunyai oleh benda untuk melakukan kerja karena letaknya, sedangkan energi kinetik ada karena massa dan kecepatan.

1.1.3.4. Hukum Kekekalan Energi

Menyatakan bahwa “energi tidak bisa dibuat atau dimusnahkan, namun bisa dirubah dari satu bentuk ke bentuk lainnya”.

1.2. Tekanan

Tekanan didefinisikan sebagai gaya per satuan luas. Satuan tekanan bergantung pada satuan gaya dan luas. Pada sistem MKS, satuan tekanan yang digunakan adalah kg/cm2 dan kg/m2. Kadang-kadang tekanan digunakan dengan satuan atmosfir dan ditulis dengan ata. Dimana 1 ata = 1 kg/cm2.

Pada sistem SI, satuan tekanan yang digunakan adalah N/mm2, N/m2, kN/m2, MN/m2 dsb. Tetapi kadang-kadang satuan tekanan yang lebih besar (bar) digunakan dimana:

1 bar = 1 X 105 N/m2

Kadang-kadang tekanan dinyatakan dengan satuan lain yang disebut Pa (Pascal) dan kPa, dimana

1 Pa = 1 N/m2 dan 1 kPa = 1 kN/m2

1.2.1. Tekanan Gauge dan Tekanan Mutlak

Semua pengukur tekanan (pressure gauge) akan membaca perbedaan antara

tekanan aktual pada suatu sistem dengan tekanan atmosfir. Bacaan yang diperoleh dari pengukur tekanan dikenal sebagai tekanan gauge, sedangkan tekanan aktual disebut tekanan absolut. Secara matematik:

Tekanan absolut = Tekanan gauge + Tekanan atmosfir.

Harga tekanan atmosfir diambil 1,033 kg/cm2 atau 1,01 bar absolut pada permukaan laut.

1.2.2. Temperatur

Temperatur adalah istilah yang penting dan didefinisikan sebagai derjat panas atau tingkat intensitas panas suatu benda. Benda yang panas disebut mempunyai temperatur yang lebih tinggi, sedangkan benda dingin mempunyai temperatur yang lebih rendah.

1.2.3. Pengukuran Temperatur

Temperatur suatu benda diukur dengan termometer. Berikut ini adalah dua skala yang umum digunakan dalam mengukur temperatur suatu benda yaitu:

1. Skala Centigrade atau Celsius; dan

2. Skala Fahrenheit.

Masing-masing skala ini didasarkan atas dua titik tetap yang dikenal dengan titik beku air atau titik es, dan titik didih air atau titik uap.

1. Skala Centigrade

Skala ini umumnya digunakan oleh ahli teknik dan ilmuwan. Titik beku air pada skala ini ditandai dengan nol, dan titik didih air ditandai dengan 100. Jarak antara titik ini dibagi dengan 100 sehingga tiap satu jarak/garis skala adalah satu derjat centigrade (ditulis dengan 0C).

2. Skala Fahrenheit

Pada skala ini, titik beku air ditandai dengan 32 dan titik didih ditandai dengan

212. Jarak antaranya dibagi 180 dan setiap jarak/garis skala mewakili satu derjat

Fahrenheit (ditulis dengan 0F).

Hubungan antara skala Centigrade dengan Fahrenheit diberikan oleh rumus :

C/100 = (F - 32)/180

1.2.4. Temperatur Absolut

Jika harga temperatur digunakan dalam persamaan yang berhubungan dengan hukum-hukum fundamental, maka harga temperatur yang digunakan sebagai rujukan adalah nol sebenarnya atau nol mutlak.

Temperatur nol mutlak/absolut diambil pada harga -273 0C atau -460 0F. Temperatur yang diukur dari nol absolut ini disebut dengan temperatur mutlak. Skala celsius mutlak disebut dengan derjat Kelvin (disingkat dengan 0K); sehingga 0K = 0C +

273. Skala absolut Fahrenheit disebut derjat Rankine (disingkat dengan 0R); dan 0R = 0F + 460.

1.3. Satuan Kalor

Jumlah panas/kalor diukur berdasarkan kuantitas untuk menaikkan temperatur dari massa air yang diketahui sebesar temperatur tertentu. Satuan-satuan berikut ini biasanya digunakan untuk mengukur jumlah kalor:

1. Calori

Adalah jumlah kalor yang diperlukan untuk menaikkan temperatur satu gram air sebesar 1 0C. Satuan yang lebih besar dari calori adalah kilokalori (kcal), yaitu jumlah kalor yang diperlukan untuk menaikkan temperatur satu kilogram air sebesar 1 0C.

Catatan : 1 kilocalori (kcal) = 1000 calori

2. Satuan kalor centigrade

Secara singkat ditulis C.H U. (Centigrade Heat Unit), adalah jumlah kalor yang diperlukan untuk menaikkan temperatur satu pound air sebesar 1 0C. Kita tahu bahwa:

1 pound = 453,6 gm

sehingga : 1 C.H.U = 3,6 calori

3. British Thermal Unit

Atau disingkat dengan B.Th.U. atau B.T.U., adalah jumlah kalor yang diperlukan untuk menaikkan temperatur satu pound air sebesar 1 0F.

Catatan : 1. Satuan calori kadang-kadang disebut gram calori (gm-cal) dan satuan kalor centigrade disebut pound calori.

2. Pada sistem MKS, satuan kalor digunakan calori atau kilocalori (ditulis cal atau

kcal).

Secara matematik, kalor yang diperlukan untuk menaikkan m kg air sebesar T derjat kelvin jika kalor spesifik adalah c (dalam kcal/kg 0K):

Q = mcT kcal

3. Pada sistem SI, satuan kalor digunakan joule atau kilojoule (ditulis J atau kJ). Secara matematik, kalor yang diperlukan untuk menaikkan m kg air sebesar T derjat kelvin jika kalor spesifik adalah c (dalam kJ/kg 0K):

Q = mcT kJ

1.3.1. Ekivalen Mekanik dari Kalor

Telah dibuktikan oleh Joule bahwa kalor dan energi mekanik bisa saling berpindah. Ia mendapatkan dari eksperimen bahwa terdapat persamaan numerik antara satuan kalor dan satuan kerja. Hubungan ini dituliskan dengan J (diambil dari nama Joule) dan dikenal sebagai ekivalen Joule atau ekivalen mekanik kalor.

Sesuai dengan persamaan ini:

1 kcal = 427 kg-m (dalam satuan MKS)

Pada sistem SI, satuan kerja adalah Joule atau kiloJoule, dan satuan kalor juga Joule atau kiloJoule, sehingga kita bisa secara langsung mengkonversikan satuan kalor ke satuan mekanikal dan sebaliknya.

1.3.2. Kalor Spesifik

Kalor spesifik suatu zat secara luas didefinisikan sebagai jumlah kalor yang diperlukan untuk menaikkan temperatur satu satuan massa suatu zat sebesar 10. Biasanya dinotasikan dengan c. Jika m kg suatu zat dengan kalor spesifikc diperlukan

untuk menaikkan temperatur sebesar t0 C, maka:

Kalor yang diperlukan = m.c.t kcal

Nilai rata-rata kalor spesifik beberapa zat diberikan oleh tabel 1. Tabel 1. Harga kalor spesifik beberapa zat.

*Padatan*	*Kalor* *Spesifik*	*Cairan*	*Kalors* *Spesifik*	*Gas pada tekanan atmosfir*	*Kalor spesisifik*
Baja Tembaga Seng Mercury Batubara Arang	0,117 0,097 0,093 0,033 0,241 0,200	Air Es Uap Minyak Bensin Alkohol Minyak parafin	1,000 0,594 0,500 0,434 0,600 0,511	Udara Karbon Dioksida Nitrogen Oksigen	0,237 0,198 0,241 0,221

1.3.3. Kapasitas Kalor

Kapasitas kalor sebuah zat bisa didefinisikan sebagai kalor yang diperlukan untuk menaikkan seluruh massa zat sebesar 10. Secara matematik:

Kapasitas kalor = m.c kalori

dimana, m = massa zat dalam gram

c = kalor spesifik zat

1.3.4. Ekivalen Air

Ekivalensi air suatu zat bisa didefinisikan sebagai jumlah air, yang memerlukan jumlah kalor yang sama ketika suatu zat dinaikkan temperaturnya sebesar 10. Secara matematik:

Ekivalensi air suatu zat = m.s gram

dimana, m = massa zat

s = kalor spesifik zat

1.4. Sistem Thermodinamika

Sistem termodinamika secara luas bisa didefinisikan sebagai luas atau ruang tertentu dimana proses termodinamika terjadi. Atau adalah suatu daerah dimana perhatian kita difokuskan dalam mempelajari proses termodinamika. Sedikit observasi akan memperlihatkan bahwa sistem termodinamika mempunyai batas sistem, dan segala sesuatu yang ada di luar batas sistem disebut lingkungan. Batas sistem ini bisa saja berupa batas tetap seperti pada tangki yang berisi gas yang terkompresi, atau batas bergerak seperti yang dijumpai pada sejumlah volume cairan di dalam saluran pipa.

1.4.1. Klasifikasi Sistem Thermodinamika

Sistem termodinamika bisa diklasifikasikan ke dalam tiga kelompok:

1. Sistem tertutup; 2. Sistem terbuka; dan 3. Sistem terisolasi.

1.4.1.1. Sistem tertutup.

Merupakan sistem massa tetap dan identitas batas sistem ditentukan oleh ruang zat yang menempatinya. Sistem tertutup ditunjukkan oleh gambar 1. Gas di dalam silinder dianggap sebagai suatu sistem. Jika panas diberikan ke silinder dari sumber luar, temperatur gas akan naik dan piston bergerak ke atas.

Gambar 1.1. Sistem termodinamika tertutup.

Ketika piston naik, batas sistem bergerak. Dengan kata lain, panas dan kerja melewati batas sistem selama proses, tetapi tidak ada terjadi penambahan atau pengurangan massa zat.

1.4.1.2. Sistem terbuka

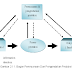
Pada sistem ini, zat melewati batas sistem. Panas dan kerja bisa juga melewati batas sistem. Gambar 2 menunjukkan diagram sebuah kompresor udara yang menggambarkan sistem terbuka ini.

Gambar 1.2. Sistem termodinamika terbuka.

Zat yang melewati batas sistem adalah udara bertekanan rendah (L.P) yang memasuki kompresor dan udara bertekanan tinggi (H.P) yang meninggalkan kompresor. Kerja melewati batas sistem melalui poros penggerak dan panas ditransfer melewati batas sistem melalui dinding silinder.

1.4.1.3. Sistem terisolasi

Adalah sebuah sistem yang sama sekali tidak dipengaruhi oleh lingkungannya. Sistem ini massanya tetap dan tidak ada panas atau kerja yang melewati batas sistem.

1.5. Sifat-Sifat Sistem

Keadaan sistem bisa diidentifikasi atau diterangkan dengan besaran yang bisa diobservasi seperti volume, temperatur, tekanan, kerapatan dan sebagainya. Semua besaran yang mengidentifikasi keadaan sistem disebut sifat-sifat sistem.

1.5.1. Klasifikasi Sifat-Sifat Sistem

Sifat-sifat termodinamika bisa dibagi atas dua kelompok umum:

1. Sifat ekstensif, dan 2. Sifat intensif.

1.5.1.1. Sifat ekstensif

Besaran sifat dari sistem dibagi ke dalam beberapa bagian. Sifat sistem, yang harga untuk keseluruhan sistem merupakan jumlah dari harga komponen-komponen individu sistem tersebut, disebut sifat ekstensif. Contohnya, volume total, massa total, dan energi total sistem adalah sifat-sifat ekstensif.

1.5.1.2. Sifat intensif

Perhatikan bahwa temperatur sistem bukanlah jumlah dari temperatur-temperatur bagian sistem. Begitu juga dengan tekanan dan kerapatan sistem. Sifat-sifat seperti temperatur, tekanan dan kerapatan ini disebut sifat intensif.

1.6. Keseimbangan Thermal

Misalkan dua benda yang berasal dari material yang sama atau berbeda, yang satu panas, dan lainnya dingin. Ketika benda ini ditemukan, benda yang panas menjadi lebih dingin dan benda yang dingin menjadi lebih panas. Jika kedua benda ini dibiarkan bersinggungan untuk beberapa lama, akan tercapai keadaan dimana tidak ada perubahan yang bisa diamati terhadap sifat-sifat kedua benda tersebut. Keadaan ini disebut keadaan kesetimbangan termal, dan kedua benda akan mempunyai temperatur yang sama.

1.7. Hukum Thermodinamika

Berikut ini ada tiga hukum termodinamika yang penting untuk diketahui:

1. Hukum thermodinamika ke Nol;

2. Hukum thermodinamika ke Satu dan

3. Hukum thermodinamika ke Dua.

1.7.1. Hukum Thermodinamika ke nol

Hukum ini berbunyi: “Jika dua benda berada dalam kondisi kesetimbangan termal dengan benda ketiga, maka benda-benda tersebut berada dalam kesetimbangan termal satu sama lainnya”.

1.7.2. Hukum Thermodinamika Ke Satu

Hukum ini berbunyi: “Kalor dan kerja mekanik adalah bisa saling tukar”. Sesuai dengan hukum ini, maka sejumlah kerja mekanik dibutuhkan untuk menghasilkan sejumlah kalor, dan sebaliknya.

Hukum ini bisa juga dinyatakan sebagai: “Energi tidak bisa dibuat atau dimusnahkan, namun bisa dirubah dari satu bentuk ke bentuk lainnya”. Sesuai dengan hukum ini, energi yang diberikan oleh kalor mesti sama dengan kerja eksternal yang dilakukan ditambah dengan perolehan energi dalam karena kenaikan temperatur. Secara matematik:

Q = ΔU +W

dimana, Q = kalor yang dipindahkan

ΔU = perubahan energi dalam

W = kerja yang dilakukan dalam satuan kalor

Persamaan di atas bisa juga ditulis dalam bentuk diferensial:

dQ = dU + dW

1.7.3. Hukum Thermodinamika ke Dua

Hukum ini berbunyi: “Ada batas tertentu dari jumlah energi mekanik, yang diperoleh dari sejumlah energi panas”.

Hukum termodinamika ini telah dinyatakan oleh Claussius dalam bentuk yang sedikit berbeda: “adalah tidak mungkin bagi mesin yang bekerja sendiri bekerja dalam proses siklik, untuk mentransfer panas dari benda dengan temperatur lebih rendah ke benda dengan temperatur yang lebih tinggi, tanpa adanya bantuan pihak luar”. Atau dengan kata lain, panas tidak bisa mengalir dengan sendirinya dari benda dingin ke benda panas tanpa bantuan pihak eksternal.

Hukum ini juga dinyatakan oleh Kelvin-Planck sebagai: “adalah tidak mungkin membuat mesin yang bekerja dalam proses siklik yang tujuan tunggalnya untuk mengkonversi energi panas ke energi kerja”. Dengan kata lain, tidak ada mesin panas sebenarnya, bekerja dalam proses siklik, bisa merubah energi panas yang diberikan

menjadi kerja mekanik. Artinya terjadi penurunan energi dalam proses menghasilkan kerja mekanik dari panas. Berdasarkan pernyataan ini, hukum kedua termodinamika kadang-kadang disebut sebagai hukum degradasi energi.

BAB II

SIFAT-SIFAT GAS SEMPURNA

Gas sempurna (atau gas ideal) bisa didefinisikan sebagai suatu keadaan zat, yang penguapannya dari kondisi cair berlangsung sempurna. Oksigen, nitrogen, hidrogen dan udara, pada batas temperatur tertentu, bisa juga disebut sebagai gas sempurna.

2.1. Hukum Gas Sempurna

Sifat fisik gas dikontrol oleh tiga variabel berikut:

1. Tekanan yang digunakan oleh gas.

2. Volume yang ditempati oleh gas.

3. Temperatur gas.

Sifat-sifat gas sempurna sempurna, yang mengalami perubahan pada variabel- variabel yang disebutkan di atas, akan mengikuti hukum-hukum berikut (diperoleh dari eksperimen):

1. Hukum Boyle.

2. Hukum Charles, dan

3. Hukum Gay-Lussac.

2.1.1. Hukum Boyle

Hukum ini diformulasikan oleh Robert Boyle pada tahun 1662. Hukum ini berbunyi,

”Tekanan mutlak suatu massa dari gas sempurna berubah secara berbanding terbalik terhadap volumenya, jika temperaturnya tetap”. Secara matematik bisa ditulis:

p ∝ 1/v

atau pv = konstan

Bentuk yang lebih berguna dari persamaan di atas adalah:

p1v1 = p2v2 = p3v3 = .... = konstan

dimana notasi 1, 2 dan 3 mengacu kepada kondisi yang berbeda.

2.1.2. Hukum Charles

Hukum ini dirumuskan oleh warga negara Perancis bernama Jacques A.C. Charles pada tahun 1787. Hukum ini dinyatakan dalam dua bentuk:

1. “Volume suatu massa gas sempurna berubah dengan berbanding langsung dengan temperatur mutlak, jika tekanan mutlaknya konstan” . Secara matematik:

v ∝ T atau v/T = konstan

atau

v1/T1 = v2/T2 = v3/T3 = Konstan

dimana notasi 1, 2 dan 3 mengacu kepada kondisi yang berbeda.

2. ”Semua gas sempurna akan menagalami perubahan volume sebesar 1/273 dari volume awalnya pada 00C untuk setiap perubahan temperatur sebesar 10 C, jika tekanan konstan”.

Misalkan, v0 = volume massa gas pada 00 C, dan

vt = volume massa gas yang sama pada t0 C

maka, sesuai dengan pernyataan di atas,

vt = vo + (1/273) vo . t = vo [(273 + t)/273] = vo . (T/To)

atau

Vt/T = Vo/To

dimana, T = temperatur mutlak dari t0 C

T0 = temperatur mutlak dari 00 C

Terlihat bahwa volume gas akan mengalami penurunan sebesar 1/273 dari volume awalnya pada setiap penurunan temperatur 10 C. Maka pada temperatur -2730 C, volume gas akan nol.1 Temperatur pada volume gas nol disebut temperatur nol mutlak.

2.1.3. Hukum Gay-Lussac

Hukum ini berbunyi: ”Tekanan mutlak dari suatu massa gas sempurna berubah berbanding langsung dengan temperatur, jika volumenya konstan”. Secara matematik:

p ∝ T atau p/T = konstan

atau

p1/T1 = p2/T2 = p3/T3 = Konstan

dimana notasi 1, 2 dan 3 mengacu kepada kondisi yang berbeda.

2.2. Persamaan Gas Umum

Pada bagian sebelumnya, telah dibicarakan tentang hukum gas dimana memberikan kita hubungan antara dua variabel, ketika variabel ketiga konstan. Dalam kondisi sebenarnya, ketiga variabel yaitu: tekanan, volume dan temperatur, berubah secara bersamaan. Untuk menyatakan kondisi ini, kedua hukum Boyle dan Charles digabung, dan memberikan persamaan gas umum.

Berdasarkan hukum Boyle :

p ∝ 1

atau

v ∝ 1

dan berdasarkan hukum Charles :

v ∝ T

Terlihat bahwa

v ∝ T

∴ pv ∝ T atau pv = CT

dimana C adalah konstanta, yang harganya tergantung pada massa dan sifat dari gas yang bersangkutan.

Bentuk yang lebih berguna dari persamaan di atas adalah :

(p1.v1)/T1 = (p2.v2)/T2 = (p3.v3)/T3 = Konstan

dimana notasi 1, 2 dan 3 mengacu kepada kondisi yang berbeda.

2.3. Hukum Joule

Berbunyi ”Perubahan energi dalam dari gas sempurna berbanding langsung dengan temperatur.” Secara matematik:

dU ∝ dT = m. C dT

dimana, m = massa gas

C = konstanta proporsionalitas, dikenal dengan kalor/panas spesifik.

2.4. Persamaan Karakteristik Gas

Adalah modifikasi dari persamaan gas umum. Jika volume (v) pada persamaan gas umum dinyatakan dalam per 1 kg gas (disebut dengan volume spesifik, dan dilambangkan dengan vs) maka konstanta C (pada persamaan gas umum) bisa diwakili dengan konstanta lain R ( pada persamaan karakteristik gas). Sehingga persamaan gas umum bisa ditulis ulang sebagai:

p.vs = RT

disini R disebut konstanta gas karakteristik atau secara sederhana disebut konstanta gas.

Untuk sembarang massa m kg, persamaan gas karakteristik menjadi:

m.p.vs = mRT

p.v = mRT (Q m.vs = v)

Catatan:

1. Satuan konstanta gas (R) bisa diperoleh sebagai berikut:

2 3

R = pv = kg/m Xm = kg m per kg 0 K

mT kgX 0 K

2. Pada satuan S.I., tekanan dalam N/m2, sehingga:

R = Nm per kg 0K = J/kg 0K (Q Nm = J)

3. Harga konstanta gas (R) berbeda untuk gas yang berbeda. Harganya pada udara atmosfir diambil

29,27 kgm/kg 0K (atau 287 J/kg 0K atau 0,287 kJ/kg 0K).

4. Persamaan pv = mRT bisa juga dinyatakan dalam bentuk lain, yaitu:

p = m RT = ρRT

(Q m/v = ρ)

dimana ρ adalah kerapatan gas yang bersangkutan.

2.4. Hukum Avogadro

Hukum ini berbunyi: ”volume yang sama dari gas-gas, pada temperatur dan tekanan yang sama, mengandung jumlah molekul yang sama”.

Maka, sesuai dengan hukum Avogadro, 1 m3 oksigen (O2) akan mempunyai jumlah molekul yang sama dengan 1 m3 hidrogen (H2) jika temperatur dan tekanannya sama. Pembuktian menunjukkan bahwa karena berat molekul hidrogen adalah 2 dan oksigen adalah 16, sehingga molekul oksigen mempunyai berat 32/2 = 16 kali berat molekul hidrogen. Karena 1 m3 kedua gas ini mempunyai jumlah molekul yang sama, dan berat molekul oksigen 16 kali dari berat molekul hidrogen, kerapatan (atau berat spesifik) oksigen adalah 16 kali dari kerapatan hidrogen. Maka, hukum Avogadro menunjukkan bahwa kerapatan dua gas berbanding lurus dengan berat molekulnya, jika gas berada pada temperatur dan tekanan yang sama.

Berat spesifik oksigen pada Normal Temperature and Pressure (disingkat N.T.P)

yaitu pada 00 C dan 1,0332 kg/cm2 absolut adalah 1,429 kg/m3.

∴ Volume spesifik oksigen (pada 1 kg) pada NTP,

vs = (1/4,29) m 3 /kg

dan volume 32 kg (atau 1 kg molekul,1 kg mol) :

= 1 x 32 = 22,4 m 3

1,429

Dengan cara yang sama bisa dibuktikan bahwa volume 1 kg mol sembarang gas pada NTP adalah 22,4 m3.

Catatan: 1 gm mol (berat molekul dinyatakan dalam gm) dari semua gas akan menempati volume 22,4 liter pada NTP.

Harga berat molekul dari beberapa gas diberikan berikut ini:

No.	Gas	Berat molekul	No.	Gas	Berat Molekul
1. 2. 3. 4.	Hidrogen (H2) Oksigen (O2) Nitrogen (N2) Karbon monoksida (CO)	2 32 28 28	5. 6. 7. 8.	Karbon dioksida (CO2) Metana (CH4) Asetilen (C2H3) Sulfur dioksida (SO2)	44 16 26 64

2.5. Konstanta Gas Universal atau Konstanta Molar

Konstanta gas universal atau konstanta molar dari gas (biasanya dilambangkan dengan Ru) adalah produk konstanta gas dan berat molekul gas. Secara matematik:

Ru = M R

Dimana, M = berat molekul gas yang dinyatakan dengan gm (yaitu gm-mol) atau kg (yaitu kg-mol)*

R = konstanta gas

Secara umum, jika M1, M2, M3 dst, adalah berat molekul dari gas yang berbeda dan R1, R2, R3 dst, masing-masing adalah konstanta gas tersebut, maka:

M1R1 = M2R2 = M3R3 ... = Ru

Catatan: 1. Harga Ru sama untuk semua gas.

2. Harganya adalah 848 kg-m/kg mol/K dalam MKS atau 8314 J/kg mol/K dalam SI.

3. Persamaan karakteristik gas (yaitu: pv = RT) bisa ditulis dalam bentuk berat molekul yaitu:

pv = MRT

2.6. Kalor Spesifik Gas

Kalor spesaifik suatu zat secara umum didefinisikan sebagai jumlah kalor yang diperlukan untuk menaikkan temperatur per satuan massanya sebesar 10 C. Semua cairan dan padatan hanya mempunyai satu harga kalor spesifik. Tetapi gas bisa mempunyai banyak kalor spesifik. (antara nol sampai tak berhingga) tergantung pada kondisi, dimana ia dipanaskan. Dua kalor spesifik berikut adalah yang penting di dalam termodinamika:

1. Kalor spesifik pada volume konstan.

2. Kalor spesifik pada tekanan konstan.

2.7. Kalor Spesifik Pada Volume Konstan

Adalah jumlah panas yang diperlukan untuk menaikkan temperatur satu satuan massa gas sebesar 10 C, jika dipanaskan pada volume konstan. Umumnya dilambangkan

dengan Cv atau Kv.

Gambar 2.1. Kalor Diberikan Pada Volume Tetap.

Misalkan sebuah gas diisikan pada sebuah kotak dengan tutup yang tetap seperti ditunjukkan gambar.

Jika sekarang kotak dipanaskan, maka temperatur dan tekanan gas dalam kotak akan naik. Karena tutup kotak tetap, maka volume gas tidak berubah.

Kalor total yang diberikan ke gas pada volume tetap adalah:

Q = massa X kalor spesifik pada vol. Konstan X

kenaikan teperatur

= m Cv (T2 – T1)

dimana, m = massa gas

T1 = temperatur awal gas

T2 = temperatur akhir gas

Jika gas dipanaskan pada volume konstan, tidak ada kerja yang dilakukan. Semua energi kalor digunakan untuk menaikkan temperatur dan tekanan gas. Dengan kata lain, semua kalor yang diberikan ada pada gas, dan menaikkan energi dalam gas.

2.8. Kalor Spesifik Pada Tekanan Konstan

Adalah jumlah kalor yang diperlukan untuk menaikkan temperatursatu satuan massa gas sebesar 10 C, jika dipanaskan pada tekanan konstan. Biasanya dilambangkan dengan Cp atau Kp.

Gambar 2.2. Kalor diberikan pada tekanan tetap.

Misalkan sebuah gas diisikan pada sebuah kotak dengan tutup yang bergerak seperti ditunjukkan gambar.

Jika sekarang kotak dipanaskan, maka temperatur dan tekanan gas dalam kotak akan naik. Karena tutup kotak bisa bergerak, maka ia akan naik ke atas, untuk mengatasi kenaikan tekanan.

Kalor total yang diberikan ke gas pada tekanan tetap adalah:

Q = massa X kalor spesifik pada tekanan konstan X kenaikan temperatur

= m Cp (T2 – T1)

dimana, m = massa gas

T1 = temperatur awal gas

T2 = temperatur akhir gas

Jika gas dipanaskan pada tekanan konstan, kalor yang diberikan ke gas dimanfaatkan untuk dua hal berikut:

1. Untuk menaikkan temperatur gas. Kalor ini berada pada gas, dan mengakibatkan kenaikan energi dalam. Secara matematis, bagian kalor ini dirumuskan:

Q1 = m.Cv.(T2 – T1)

2. Untuk melakukan kerja luar/eksternal selama ekspansi. Secara matematis, ditulis:

Q2 = p(v2 – v1) (dalam kalor mekanik)

Q2 = p(v2 – v1) / J (dalam satuan kalor)

Terlihat bahwa kalor spesifik pada tekanan konstan lebih tinggi dari pada kalor spesifik pada volume konstan.

Catatan: 1. kerja luar yang dilakukan bisa juga dinyatakan dengan :

W = p(v2 – v1) / J = (pv2 – pv1) / J

= mR(T2 − T1 )/J

2. Dalam satuan S.I., persamaan di atas menjadi:

W = p(v2 − v1 ) = mR(T2 − T1 )

2.9. Hubungan Antar Kalor Spesifik

Misalkan sebuah kotak dipanaskan pada tekanan konstan. Dan notasi sebagai berikut:

m = massa gas

T1 = temperatur mutlak awal gas T2 = temperatur absolut akhir gas v1= volume awal

gas

v2 = volume akhir gas

Cp = kalor spesifik pada tekanan konstan

Cv = kalor spesifik pada volume konstan

p = tekanan konstan

Kita tahu bahwa kalor yang diberikan ke gas pada tekanan konstan:

Q = m Cp (T2 – T1)

• Kalor yang digunakan untuk kerja luar:

W = p(v2 – v1) / J ....( i )

dan kenaikan energi dalam:

ΔU = m Cv (T2 – T1) ... (ii)

Kita tahu bahwa :

Q =W+ ΔU .... (iii)

Sehingga:

m Cp (T2 – T1) = p(v2 – v1) / J + m Cv (T2 – T1) …(iv)

Dengan menggunakan persamaan gas (pv = mRT), maka :

pv1 = mRT1

pv2 = mRT2

∴ p(v1-v2) = mR (T2 – T1)

Substitusikan harga p(v2 – v1) pada persamaan (iv):

m Cp (T2 – T1) = mR (T2 – T1) /J + m Cv (T2 – T1)

Cp = R/J + Cv ... (v)

atau

Cp - Cv = R/J ... (vi)

Persamaan di atas bisa ditulis dengan :

Cp - Cv = R/J

Cv (γ − 1) = R/J dimana : γ = Cp /Cv

Cv = R/J (γ − 1) ... (vii)

Catatan :

1. Adalah hasil penting, membuktikan bahwa karakteristik konstanta gas adalah

sama dengan perbedaan kedua kalor spesifik.

2. Dalam S.I. persamaan di atas menjadi :

Cv = R/(γ − 1)

dimana R adalah konstanta gas, dan nilainya diambil 0,287 kJ/kg 0K.

2.10. Rasio Kalor Spesifik

Rasio dua kalor spesifik (yaitu Cp/Cv) dari gas adalah konstanta penting di dalam termodinamika dan dilambangkan dengan γ. Rasio ini dikenal juga dengan indeks

adiabatis. Karena Cp selalu lebih besar dari Cv , harga γ selalu lebih besar dari satu.

Seperti telah ditulis sebelumnya bahwa :

Cv = R/J + Cv

Cp/Cv = 1 + R/J.Cv

γ = 1 + R/J.Cv

Dalam satuan SI ditulis :

γ = 1 + R/Cv

Harga Cv dan Cp untuk beberapa gas pada temperatur antara 150 sampai 200 diberikan oleh tabel berikut:

		Cp Satuan Satuan SI MKS kJ/kg 0K Kcal/kg 0K		Cv Satuan MKS Kcal/kg 0K	Satuan SI γ = Cp/Cv kJ/kg 0K

No.	Nama gas
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.	Udara Karbon dioksida (CO2) Oksigen (O2) Nitrogen (N2) Amonia (NH3) Karbon monoksida (CO) Hidrogen (H2) Argon (A) Helium (He) Metana (CH4)	0,240 0,202 0,218 0,249 0,520 0,250 3,405 0,125 1,250 0,518	1,005 0,846 0,913 1,043 2,177 1,047 14,257 0,523 5,234 2,169	0,172 0,157 0,156 0,178 0,404 0,179 2,420 0,075 0,753 0,394	0,720 0,657 0,653 0,745 1,692 0,749 10,133 0,314 3,153 1,650	1,40 1,29 1,39 1,40 1,29 1,40 1,40 1,67 1,66 1,31

2.11. Enthalpi

Fungsi termodnamika khusus diperkenalkan untuk kemudahan. Fungsi tersebut yang paling sederhana adalah enthalpi, H, dan didefinisikan dengan:

H = U + PV

Jika terjadi perubahan pada sistem, perubahan enthalpi:

dH = dU + d (PV)

Fungsi termodnamika khusus diperkenalkan untuk kemudahan. Fungsi tersebut yang paling sederhana adalah enthalpi, H, dan didefinisikan dengan:

H = U + PV

Jika terjadi perubahan pada sistem, perubahan enthalpi:

dH = dU + d(PV)

BAB III

PROSES TERMODINAMIKA

GAS SEMPURNA

Proses pemanasan dan ekspansi gas secara umum bisa didefinisikan sebagai proses termodinamika. Dari pengamatan, sebagai hasil dari aliran energi, perubahan terjadi pada berbagai sifat gas seperti tekanan, volume, temperatur, energi spesifik, enthalpi spesifik, dsb. Proses termodinamika bisa terjadi dalam berbagai keadaan, tetapi proses-proses berikut adalah beberapa dari proses termodinamika yang penting.

1. Proses volume konstan.

2. Proses tekanan konstan.

3. Proses hiperbolik.

4. Proses isothermal (proses temperatur konstan).

5. Proses adiabatik atau proses isentropik.

6. Proses politropik.

7. Proses ekspansi bebas.

8. Proses Throttling.

Catatan : 1. Proses yang disebutkan di atas juga bisa diaplikasikan pada proses pendinginan dan kompresi gas. Pendinginan merupakan pemanasan negatif, dan kompresi adalah ekspansi negatif.

2. Dalam proses termodinamika, salah satu hal yang ingin diketahui adalah mencari jumlah kerja yang dilakukan selama proses.

3.1. Proses Volume Konstan

Seperti telah disebutkan sebelumnya bahwa gas yang dipanaskan pada volume konstan, temperatur dan tekanannya akan naik. Karena tidak ada perubahan volume, maka tidak ada kerja yang dilakukan oleh gas.

Semua panas yang diberikan disimpan di dalam molekul gas dalam bentuk energi dalam. Perlu di catat bahwa proses ini diatur oleh hukum Gay Lussac.

Gambar 3.1. Proses volume konstan.

Seandainya ada m kg gas yang dipanaskan pada volume konstan dari temperatur awal T1 ke temperatur akhir T2. Proses ini ditunjukkan oleh diagram p-v pada gambar 1.

Kita tahu bahwa:

Q = ΔU + W

Atau :
Q = ΔU (karena W = 0)
Persamaan energi dalam adalah:

ΔU = m.Cv (T2 – T1)

Jadi kalor yang diberikan:

Q =ΔU = m.Cv (T2 – T1)

3.2. Proses Tekanan Konstan

Ketika gas dipanaskan pada tekanan konstan, temperatur dan volumenya akan meningkat. Karena ada perubahan volume, kalor yang diberikan dimanfaatkan untuk menaikkan energi dalam gas, dan juga untuk melakukan kerja luar. Perlu dicatat bahwa proses ini mengikuti hukum Charles.

Gambar 2.

Proses tekanan konstan.

Seandainya ada m kg gas yang dipanaskan pada tekanan konstan dari temperatur awal T1 ke temperatur akhir T2. Proses ini ditunjukkan oleh diagram p-v pada gambar 2.

Kita tahu bahwa kalor yang diberikan ke gas pada tekanan konstan:

Q = m.Cp (T2 – T1)

Kenaikan energi dalam adalah:

ΔU = m.Cv (T2 – T1)

Dan kerja yang dilakukan selama proses:

W = luas daerah di bawah garis 1-2

W = p(v2–v1) (dalam satuan kerja)

W = [p(v2–v1)]/J (dalam satuan kalor)

W =[pv2 – pv1)]/J = [ mRT2 − mRT1 ]/J

= [mR(T2 −T1 )]/J

(dalam satuan kalor)

Catatan: Jika gas didinginkan pada tekanan konstan, maka akan berupa kompresi. Jelas bahwa selama pendinginan, temperatur dan volume berkurang dan kerja dikatakan ’dilakukan pada gas’. Dalam hal ini, kalor yang dilepaskan oleh gas: