MODUL I
MENGENAL WINQSB
A. MAKSUD DAN TUJUAN
1. Maksud
Mengenal, memahami dan mencoba
contoh-contoh program yang akan dibuat dengan menggunakan WINQSB
2. Tujuan
Agar mahasiswa mampu menggunakan
perintah-perintah pada WINQSB untuk menyelesaikan masalah-masalah Riset
Operasi.
B. WINQSB
WINQSB, adalah
sebuah paket program
under Windows, yang
terdiri dari berbagai sub menu seperti gambar berikut ini
:
Gambar 1.1. Tampilan WINQSB untuk Linear Programming.
A. MENJALANKAN WINQSB
1.Pilihlah Linear and
Integer Programming, maka
pada layer akan
muncul gambar sebagai berikut :
2. Pilihlah
File
dan pilih New Problem
3.
Setelah File
dan New Problem
dipilih maka akan
muncul gambar sebagai berikut:
4. Isikan
Problem Title misalnya Contoh1 Isikan Number Of Variables = 2
Isikan Number Of Contraints = 3
Object Criterion pilih
Maximization
Data Entry Format, pilih
Spreadsheet Matrix Form Default Variable Type, pilih Nonnegative Continous
Dengan contoh sebagai berikut :
Maksimum Z = 2X1 + X2
Batasannya : 12X1 + X2 <= 36
3X1 + 2X2
<= 12
X1 + 2X2 <= 36
Maka, akan muncul gambar sebagai berikut :
Maka, akan muncul gambar sebagai berikut :
Kemudian
klik OK jika pengisian
telah selesai, maka
akan muncul gambar sebagai berikut :
5.
Jika pengisian telah
selesai, kita dapat
mengetahui hasilnya dengan
memilih menu Solve and Analyse, yang mempunyai sub menu seperti gambar
berikut ini :
-
Jika
anda memilih Solve
the Problem, maka
akan menghasilkan, hasil akhir
dari contoh program
yang dibuat, seperti
gambar berikut ini :
Sedangkan untuk melihat hasil yang
lainnya, anda bisa memilih menu Result, seperti gambar berikut ini :
Anda bisa menampilkan kesimpulan dari contoh program yang anda buat dengan
memilih Solution
Summary, atau anda bisa memilih hasil akhir dari contoh
program yang anda
buat dengan memilih
Final Simplex Tableau. Seperti gambar-gambar
berikut ini.
-
Jika anda memilih Solve and Display Steps, maka akan menampilkan
iterasi-iterasi yang
harus dilakukan sampai
mencapai hasil akhir. Seperti gambar berikut ini :
untuk melanjutkan
pada iterasi berikutnya,
anda memelih menu Simplex
Iteration dan klik sub menu Next Iteration.
Untuk keluar
dari Solve and Analyse
yang telah anda
lakukan, pilih menu File dan
Exit,
maka akan kembali pada problem
solving yang sudah anda buat, seberti gambar berikut ini :
D. SIMPAN DAN MEMBUKA
Untuk menyimpan data-data yang
sudah dimasukkan (solve problem), pilih menu File dan pilih Save
Problem, seperti gambar berikut ini :
Setelah anda memilih
Save Problem,
maka akan muncul
kotak dialog, anda
tinggal memilih direktori tempat data anda akan disimpan, seperti gambar
berikut ini :
Untuk memanggil kembali, data yang telah anda simpan,
kembali anda memilih menu File dan pilih Load Problem, maka akan muncul gambar
seperti berikut :
Setelah anda memilih Load Problem, maka akan muncul kotak
dialog sebagai berikut dan anda tinggal memilih nama data yang anda simpan
tadi.
E. CETAK
Untuk mencetak
hasil dari Solve
and Analyse yang
telah anda buat,
kembali anda memilih menu File dan
klik Print,
seperti gambar berikut ini :
F. EDIT
Untuk mengedit data-data
yang telah anda
isikan, bisa langsung anda
lakukan pada saat data yang telah diketik muncul kembali
pada Matrix Form seperti gambar berikut
ini :
Sedangkan untuk mengedit yang lain, anda pilih menu Edit,
seperti gambar berikut ini :
1. Mengedit Problem
Name, digunakan untuk
mengganti title yang telah
ditulis, maka akan muncul kotak
dialog sebagai berikut :
2. Mengedit Variabel Name,
digunakan untuk mengganti
variable bawaan dari WINQSB, maka akan muncul kotak dialog
sebagai berikut :
3. Mengedit Constraint Name,
digunakan untuk menggantikan Constraint bawaan dari WINQSB,
maka akan muncul kotak dialog sebagai berikut :
G. METODE GRAFIK
Jika menyelesaikan masalah Linear Programming dengan metode
Grafik pada WINQSB, maka caranya adalah sebagai berikut :
1.
Pada menu pilih Solve and
Analyse, dan klik Graphic Method,
seperti gambar berikut :
2.
Setelah Graphic
Method dipilih, maka akan muncul tampilan sebagai berikut :
3.
Anda
tinggal mengklik tombol
OK, maka grafik
yang anda inginkan
akan muncul, seperti gambar
berikut ini :
MODUL III
METODE SIMPLEKS
MODUL IV
MASALAH TRANSPORTASI
MODUL V
MASALAH PENUGASAN
MODUL VI
ANALISA JARINGAN
Palembang, Makasar dan Denpasar). Rute yang dapat ditempuh terlihat pada tabel
2.
Setelah Graphic
Method dipilih, maka akan muncul tampilan sebagai berikut :
3.
Anda
tinggal mengklik tombol
OK, maka grafik
yang anda inginkan
akan muncul, seperti gambar
berikut ini :
D. PRAKTIKUM
1.
Pada praktikum ini, praktikan diminta untuk mencoba
semua perintah dan mencoba semua contoh
seperti yang tertulis di atas.
2.
Masukan data dibawah ini dengan menggunakan WINQSB dan
cetaklah input datanya dan juga Final Tabelnya saja
Maksimum
|
Z = 6A + 2B +
C
|
Batasannya
|
2A <=
35
A + 6B +
2C <= 37
6A + 9C
<= 57
|
MODUL II
METODE GRAFIK
A. MAKSUD DAN TUJUAN
1.
Tujuan
Menyelesaikan
masalah Program Linear pada Riset Operas dengan menggunakan metode grafik.
2.
Maksud
Agar mahasiswa mampu dan dapat
menyelesaikan masalah Linear Programming dengan metode grafik.
B. TEORI
Dengan menggunakan
Linear Programming pada
WINQSB, anda dapat menyelesaikan suatu masalah dengan
menggunakan metode grafik yang telah tersedia dengan sangat mudah.
Berikut ini
adalah satu contoh
penyelesaian masalah menggunakan
metode grafik.
Maksimum = 50X1 + 60X2
2X1 +
3X2 <= 180
3X1 + 2X2
<= 150
Problem ini
mempunyai dua variable X1 dan X2, karena itu harus ditentukan harga X1 dan X2,
yang memenuhi sistem batasan.
Berdasarkan
contoh masalah tersebut
di atas, kita
dapat menyelesaikannya dengan
cara sebagai berikut :
1.
Masuk dahulu ke WINQSB.
Pilih Linear and Integer Linear
Programming
2.
Pilih Menu File dan
klik sub menu New
Problem, maka akan
muncul tampilan sebagai berikut :
3.
Isikan Problem Title,
Number of Variables
dan Number of Contraints, kemudian klik tombol OK, maka akan muncul tampilan sebagai berikut :
4. Kemudian
pilih menu Solve and
Analyze, kemudian pilih Graphic
Method, makan akan
muncul tampilan sebagai berikut :
5.
Klik tombol OK,
maka akan muncul hasilnya sebuah grafik sebagai berikut :
6. Masih
dengan menggunakan WINQSB,
anda juga dapat
menghasilkan grafik- grafik dalam
bentuk lain, dengan
memilih menu Utilities
dan klik Graph/Chart, seperti tampilan gambar berikut
ini :
7.
Kemudian
anda pilih menu
Gallery, maka akan
muncul tampilan gambar
seperti berikut :
Dan jika
anda memilih Column
-2D, maka akan
muncul tampilan grafik
seperti berikut :
Dan misalnya
anda memilih Pie-2D,
makan akan muncul
tampilan grafik seperti berikut :
8.
Hasil dari grafik
yang telah dibuat
dapat diubah warna-warnanya sesuai
dengan yang anda inginkan
dengan memilih menu
Options dan klik
Change XY Ranges and Colors, maka akan muncul tampilan
sebagai berikut :
Anda tinggal menggubah warna-warnanya sesuai dengan yang
anda inginkan, jika telah selesai anda memilih, anda tinggal mengklik tombol
OK.
C. PRAKTEK
1.
Hitunglah
pemecahan optimal dari
masalah yang formulasinya
adalah sebagai berikut :
Maksimum
Z = 3X1 + 4X2
2X1 + X2
<= 6
2X1 + 3X2 <= 9
X1 >= 0 ; X2 >= 0
2. Perusahaan
Disk merencanakan untuk
memproduksi dua macam
produk dan sekaligus menjualnya.
Kedua produknya adalah produk A dan produk B. Harga jual per unit produk A
adalah Rp. 500,- dan produk B adalah Rp. 600,-. Biaya variable per
unit produk A
adalah Rp. 250.,
dan produk B
adalah Rp. 350,-. Setiap produk
A memerlukan bahan baku 10 unit dan tenaga kerja langsung 5 jam. Setiap
produk B memerlukan
bahan baku 15
unit dan tenaga
kerja langsung 10 jam.
Permintaan potensial terhadap
produk A dan
B maksimal sebesar 40 dan 50 unit
per bulan. Bahan baku yang tersedia 350 unit per bulan dan tenaga kerja
langsung yang tersedia adalah 260 jam per bulan. Hitunglah banyaknya produk
A dan B yang sebaiknya
dihasilkan setiap bulan
agar diperoleh laba maksimum.
D. TUGAS
1. Kerjakan
persoalan di atas secara metode grafik
MODUL III
METODE SIMPLEKS
A.
MAKSUD DAN
TUJUAN
1. Tujuan
Menyelesaikan masalah Program
Linear untuk kasus maksimisasi dan minimisasi
dengan menggunakan metode simplek.
2. Maksud
Agar mahasiswa
mampu menggunakan WINQSB
untuk menyelesaikan
masalah-masalah Program Linear dengan menggunakan metode simplex.
B.
TEORI
Meskipun problem program linear dapat diselesaikan
secara grafik seperti yang telah
kita lakukan pada
praktek sebelumnya, akan
tetapi hampir seluruh
problem program linier sesungguhnya
tidak dapat diselesaikan
dengan menggunakan metode grafik, karena pada umumnya program
linier mempunyai lebih dari 3 variabel.
Oleh karena itu
George Dantzig pada
tahun 1947 mengajukan
satu metode yang paling berhasil
untuk menyelesaikan problem program linier yang disebut metode simpleks.
Metode
simpleks adalah suatu
prosedur ulang yang
bergerak dari satu
jawab layak basis ke
jawab berikutnya sedemikian
rupa hingga harga
fungsi tujuan terus menaik, proses ini akan berkelanjutan
sampai dicapai jawab optimal yang memberikan harga maksimum.
Dengan
menggunakan WINQSB, anda dengan sangat
mudah dapat menyelesaikan masalah
dengan menggunakan metode
simpleks. Misalnya ada
contoh kasus sebagai berikut :
Maksimum F = 2X1 + X2 + 3X3
X1 + X2 + 2X3
|
<= 400
|
2X1 + X2 + X3
|
<= 500
|
X1, X2, X3 >= 0
Dari contoh di
atas dapat dengan
mudah diselesaikan dengan
menggunakan WINQSB, caranya adalah sebagai berikut :
1. Masuk dahulu ke WINQSB.
Pilih Linear and Integer Linear
Programming
2. Pilih Menu File
dan klik sub
menu New Problem, maka
akan muncul tampilan sebagai berikut :
3. Isikan Problem Title,
Number of Variables
dan Number of
Contraints, kemudian klik tombol OK, maka akan muncul tampilan sebagai berikut :
4. Jika pengisian telah selesai, kita dapat mengetahui
hasilnya dengan memilih menu Solve and Analyse, pilihlah Solve
the Problem, maka akan menghasilkan, hasil akhir dari contoh program yang
dibuat, seperti gambar berikut ini :
Sedangkan untuk melihat hasil
yang lainnya, anda bisa memilih menu Result,
seperti gambar berikut ini :
Anda bisa menampilkan kesimpulan dari contoh program yang anda buat dengan
memilih Solution
Summary, atau anda bisa memilih hasil akhir dari contoh
program yang anda
buat dengan memilih
Final Simplex Tableau. Seperti gambar-gambar
berikut ini.
1.
Untuk mencetaknya anda pilih menu File dan klik Print.
C. PRAKTEK
1.
Selesaikan persoalan linier berikut dengan menggunakan
metode simpleks
Maksimumkan Z =
150X1 + 100X2 + 75X3
Batasan-batasan
X1 + X2 + 2X1 <=
600
2X1 + X2 + 2X3 <=
1000
X1,
X2 >= 0
2.
Pabrik Alfa dan
Beta menghasilakn dua
jenis produksi P1
dan P2, dari
dua bahan baku yaitu
Alfa dan Beta.
Informasi yang tersedia
untuk menyelesaikan persoalan
Koefisien InputO
P1
|
utput
P2
|
Bahan baku yang tersedia
|
|
Alfa
|
10
|
20
|
800
|
Beta
|
20
|
10
|
1000
|
Untung
Bersih
|
300
|
200
|
produksi adalah :
Selesaikan persoalan dengan menggunakan
metode simpleks untuk memperoleh rencana produksi yang optimal.
MODUL IV
MASALAH TRANSPORTASI
A. MAKSUD DAN TUJUAN
1.
Tujuan
Menyelesaikan masalah
Pendistribusian pada Riset Operasi dengan menggunakan metode transportasi
2.
Maksud
Agar mahasiswa mampu menyelesaikan
masalah transportasi dengan menggunakan WINQSB.
B. TEORI
Dengan menggunakan
modul Network Modeling pada
WINQSB, anda dapat menyelesaikan suatu masalah
transportasi dengan sangat mudah.
Berikut ini
adalah satu contoh
penyelesaian masalah transpotasi
PT. ABC memiliki pabrik di 2 tempat, yaitu kota X dan
kota Y, sedangkan daerah pemasaranya meliputi daerah a, b dan c. kapasitas produksi di pabrik dikota X
adalah 300 unit dan kapasitas produksi pabrik di kota Y adalah 500, permintaan
produk untuk daerah a, b, c , masing –masing adalah 150, 300 dan 350 unit.
Biaya kirim
produk dari pabrik di kota X ke daerah a, b, c , masing masing adalah RP10,
Rp12, dan Rp8. Sedangkan biaya kirim dari kota Y ke daerah a, b, c
masing-masing adalah Rp7, Rp10.
PT ABC ingin
mengetahui berapa banyak produk yang harus dikirim dari pabrik X dan Y ke
daerah pemasaran agar di peroleh biaya minimum.
Bila dinyatakan dalam bentuk table akan tampak seperti
berikut:
Dari/ke
|
a
|
b
|
c
|
produksi
|
X
|
10
|
12
|
8
|
300
|
Y
|
7
|
10
|
14
|
500
|
permintaan
|
150
|
300
|
350
|
Penyelesaiannya adalah sebagai
berikut :
1.
Pilih Network Modeling,
lalu pilih ,menu file, New Problem , Lalu pilih type Transportation Problem.
a.
Pada bagian Problem title diisi dengan Masalah Transportasi.
b.
Pada kolom Number of Source diisi dengan 2.
c.
Pada kolom Number of Distination diisi dengan 3
2.
klik ok sehingga
muncul tampilan untuk menginput data masalah Network seperti berikut ini :
3.
Ubahlah lokasi asal dan lokasi tujuan sesuai
dengan soal diatas, dengan meng klik
menu Edit, Node Names, lalu gantilah, jika sudah selesai klik OK.
4.
Inputkan data yang ada pada table diatas, kemudian
simpan di folder D:\data\namamu ( dengan klik menu File, Save problem). Dengan nama lat_trans.
5.
Klik Menu File, Load problem, lalu pilihlan
lat_trans.net
6.
klik menu Solve
and Analyze, lalu pilih Solve the
Problem, maka akan muncul hasilnya seperti berikut :
Dari tampilan tersebut diketahui
bahwa solusi optimal untuk pengiriman
produk dari pabrik X ke daerah c
sebanyak 300 unit ( per unit Rp8
sehingga total biaya Rp2.400),
Dari pabrik Y ke daerah a sebanyak 150
unit, dari pabrik Y ke daerahsebanyak 300 unit dan dari pabrik Y ke daerah c
sebanyak 50 unit. Biaya total dari pabrik Y ke daerah a,b, dan c masing-masing
Rp1.050, Rp3000 dan Rp700, sehingga biaya pengiriman keseluruhan adalah Rp
7.150.
Untuk menampilkan solusi dalam bentuk grafik, klik menu Result, Grapich Solution.
C. PRAKTEK
1. Carilah penyelesaian optimum
masalah berikut ini:
Dari/ke
|
Gudang A
|
Gudang B
|
Gudang C
|
Kapasitas pabrik
|
Pabrik W
|
20
|
5
|
8
|
90
|
Pabrik H
|
15
|
20
|
10
|
60
|
Pabrik P
|
25
|
10
|
19
|
50
|
Kebutuhan gudang
|
50
|
110
|
40
|
200
|
2. Kapasitas
produksi pabrik A,B, C tiap bulan masing masing adalah 150 ton, 40 ton dan 80 ton. Sedangkan gudang 1, 2, dan 3 masing masing dapat
menampung 110 ton, 70 ton dan 90 ton perbulan. Biaya pengiriman barang ke
gudang adalah:
a.
dari Pabrik A ke gudang 1 Rp 27000, gudang 2 Rp 23000
dan gudang 3 Rp 31000
b. dari
Pabrik B ke gudang 1 Rp 10000, gudang 2 Rp 45000 dan gudang 3 Rp 40000
c. dari
Pabrik C ke gudang 1 Rp 30000, gudang 2 Rp 54000 dan gudang 3 Rp 35000 carilah
penyelesaian unruk biaya pengiriman terkecil !
MODUL V
MASALAH PENUGASAN
A. MAKSUD DAN TUJUAN
1.
Tujuan
Menyelesaikan masalah penugasan
pada Riset Operasi dengan menggunakan metode Assigment agar optimal.
2.
Maksud
Agar mahasiswa mampu menyelesaikan masalah Penugasan. dengan
menggunakan WINQSB
B. TEORI
Dengan menggunakan
modul Network Modeling pada WINQSB, anda
dapat menyelesaikan suatu masalah penugasan dengan sangat mudah.
Berikut ini
adalah satu contoh
penyelesaian masalah penugasan
PT. ABC memiliki tiga orang karyawan pada bagian
desain, ketiga karyawan itu adalah Budi, Bima dan Agus. Ketiga karyawan itu
diminta untuk membuat 3 buah desain produk yaitu produk a, b dan c. Budi
memerlukan waktu 4 hari untuk merancang produk a, 4 hri untuk merancang produk
b dan 3 hari untuk merancang produk c. Bima memerlukan waktu 8 hari untuk
merancang produk a, 7 hari untuk produk b dan 6 hari untuk produk c, sedangkan
agus memerlukan waktu 2 hari untuk merancang produk a, 3 hari untuk produk b,
dan 1 hari untuk merancang produk c
PT ABC ingin mem\ncari waktu tersingkat, maka
tugas desain itu dibagi pada 3 karyawan, maka carilah kepada siapa saja yang
perlu di tugasi untuk masing-masing produk.
Bila dinyatakan dalam bentuk tabel akan tampak seperti
berikut:
produk/orang
|
Budi
|
Bima
|
Agus
|
a
|
4
|
8
|
2
|
b
|
4
|
7
|
3
|
c
|
3
|
6
|
1
|
Penyelesaiannya adalah sebagai
berikut :
1.
Pilih Network
Modeling, lalu pilih ,menu file, New Problem , Lalu pilih type Assignment Problem.
a.
Pada bagian Problem title diisi dengan Masalah Penugasan.
b.
Pada kolom Number of Objects diisi dengan 3.
c.
Pada kolom Number of
Assignment diisi dengan 3
d.
Pada option Object Criterion pilih Minimazion
2.
klik ok
sehingga muncul tampilan untuk menginput data masalah Network seperti berikut ini :
3.
Ubahlah lokasi asal dan lokasi tujuan sesuai
dengan soal diatas, dengan meng klik
menu Edit, Node Names, lalu gantilah, jika sudah selesai klik OK.
4.
Inputkan data yang ada pada table diatas, kemudian
simpan di folder D:\data\namamu\ ( dengan klik menu File, Save problem). Dengan nama lat_tugas.
5.
Klik Menu File, Load problem, lalu pilihlan
lat_tugas.net
6.
klik menu Solve
and Analyze, lalu pilih Solve the
Problem, maka akan muncul hasilnya seperti berikut :
Dari tampilan tersebut diketahui bahwa solusi optimal untuk
pengasan desain produk
Adalah untuk produk a diberikan kepada
Agus, produk b kepada Budi dan produk c kepada Bima. Waktu yang dibutuhkan
untuk ketiga desain produk a, b dan c, masingmasing adalah 2 hari, 4 hari dan 6
hari.
Untuk menampilkan solusi dalam bentuk grafik, klik menu Result, Grapich Solution.
C. PRAKTEK
1.
Karyawan-pekerjaan
|
1
|
2
|
3
|
4
|
Raihan
|
150
|
200
|
180
|
220
|
Hamdan
|
140
|
160
|
210
|
170
|
Hasan
|
250
|
200
|
230
|
200
|
Dzakwan
|
170
|
180
|
180
|
160
|
Carilah penugasan yang tepat
agar biaya produksi minimum !!!
2.
mesin-produk
|
A
|
B
|
C
|
D
|
1
|
6
|
7
|
10
|
9
|
2
|
2
|
8
|
7
|
8
|
3
|
8
|
9
|
5
|
12
|
4
|
7
|
11
|
12
|
3
|
Carilah penugasan yang tepat agar
jumlah produk yang dihasilkan maksimum !!!
3. 5 proyek pemerintah
dalam APBN 2009/2010 akan segera dilaksanakan di 5 propinsi. Dari
Pemerintah pusat, disediakan 5 tim kerja yang akan melaksanakan proyek
tersebut. Biaya dari proyek tersebut adalah sebagai berikut :
Tim Kerja
|
Jalan Raya
|
Terminal Bis
|
Rumah
Sakit
|
Sekolah Dasar
|
Taman Wisata
|
Tim Satu
|
3
|
8
|
2
|
10
|
15
|
Tim Dua
|
8
|
7
|
2
|
9
|
13
|
Tim Tiga
|
6
|
4
|
2
|
7
|
12
|
Tim Empat
|
8
|
4
|
2
|
3
|
11
|
Tim Lima
|
9
|
10
|
6
|
9
|
17
|
Buatlah penugasan masing-masing tim untuk mengerjakan
masing-masing proyek. Berapa biaya yang harus dikeluarkan?
MODUL VI
ANALISA JARINGAN
A. MAKSUD DAN TUJUAN
1.
Tujuan
Menyelesaikan masalah
Perencanaan Pekerjaan pada Riset Operasi
dengan menggunakan metode Jalur terpendek
2.
Maksud
Agar mahasiswa mampu menyelesaikan
masalah Jalur terpendek dengan menggunakan WINQSB.
B. TEORI
Dengan menggunakan
modul Network Modeling pada
WINQSB, anda dapat menyelesaikan suatu masalah Jalur
terpendek dengan sangat mudah.
Berikut ini
adalah satu contoh
penyelesaian masalah Jalur
Terpendek
PT. ABC memiliki armada kendaraan
yang berpusat di Palembang, yang setiap saat dipakai untuk menjangkau kota-kota
produksi (yaitu Jakarta dan Yogyakarta) dan cabang-cabang perusahaan (yaitu dibawah ini:
Dari/ke
|
Surabaya
|
Jakarta
|
Palembang
|
Denpasar
|
Yogyakarta
|
Makasar
|
Surabaya
|
1100
|
220
|
900
|
|||
Jakarta
|
1100
|
150
|
||||
Palembang
|
150
|
1300
|
1000
|
|||
Denpasar
|
1300
|
800
|
||||
Yogyakarta
|
220
|
1000
|
800
|
|||
Makasar
|
900
|
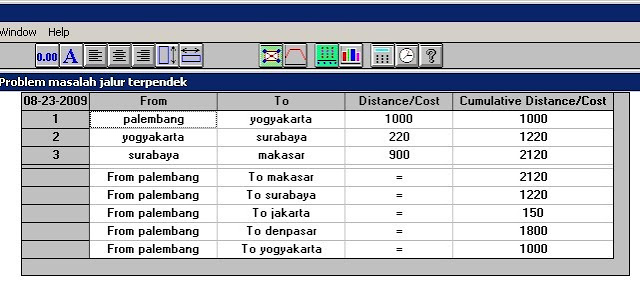
PT ABC ingin mengirim barang dari Palembang ke Makasar, agar
jarak yang ditempuh minimum, jalur manakan yang harus di tempuh ??
Penyelesaiannya adalah sebagai
berikut :
1.
Pilih Network
Modeling, lalu pilih ,menu file, New Problem , Lalu pilih type Shortest
Path Problem.
a.
Pada bagian Problem title diisi dengan Masalah Jalur Terpendek
b.
Pada kolom Number of Nodes diisi dengan 6..
2.
klik ok
sehingga muncul tampilan untuk menginput data masalah Network seperti berikut
ini :
3. Ubahlah lokasi asal dan lokasi tujuan sesuai
dengan soal diatas, dengan meng klik
menu Edit, Node Names, lalu gantilah, jika sudah selesai klik OK.
4. Inputkan data yang ada pada table diatas, kemudian
simpan di folder D:\data\namamu ( dengan klik menu File, Save problem). Dengan nama lat_jalur. 5. Klik Menu File, Load problem, lalu
pilihlan lat_jalur.net
5. klik menu Solve and Analyze, lalu pilih Solve the Problem, maka akan muncul
form untuk memilih tempat mulai dan tempat tujuan .untuk rempat mulai pilihlah
Palembang sedangkan untuk tujuan pilih Makasar. Lalu klik ok
Makan akan muncul tabel penyelesaian seperti gambar di
bawah ini:.
Dari tampilan tersebut diketahui
bahwa solusi optimal untuk pengiriman produk dari
Palembang
ke Makasar adalah dengan rute
PalembangYogyakarta, YogyakartaSurabaya dan Surabaya-Makasar. Jarak yang
ditempuh 2120.
Untuk menampilkan solusi dalam bentuk grafik, klik menu Result, Grapich Solution.
C. PRAKTEK
1. Perusahaan X akan memasang jaringan telpon di daerah A.
biaya pemasangan dari masing-masing titik dapat dilihat pada tabel dibawah. Hitunglah berapa biaya yang paling minim yang harus dikeluarkan perusahaan
untuk menghubungkan semua titik agar semua warga dapat menikmati jaringan
telpon.
jalur
|
Titik awal
|
Titik tujuan
|
biaya
|
Jalur 1
|
1
|
2
|
5
|
Jalur 2
|
1
|
3
|
6
|
Jalur 3
|
1
|
4
|
6
|
Jalur 4
|
1
|
5
|
5
|
Jalur 5
|
2
|
6
|
7
|
Jalur 6
|
3
|
7
|
5
|
Jalur 7
|
4
|
7
|
7
|
Jalur 8
|
5
|
8
|
4
|
Jalur 9
|
6
|
7
|
1
|
Jalur 10
|
7
|
9
|
6
|
Jalur 11
|
8
|
9
|
2
|
Biaya : x Rp 100.000
MODUL VII
P E R T-CPM
A. MAKSUD DAN TUJUAN
1.
Tujuan
Menyelesaikan masalah jaringan
pada Riset Operasi dengan menggunakan metode PERT
2.
Maksud
Agar mahasiswa mampu memahami dan
menyelesaikan masalah jaringan kerja. degan menggunakan WINQSB
B. TEORI
Dengan menggunakan
modul PERT/CPM pada
WINQSB,anda dapat menyelesaikan suatu
masalah analisa kegiatan dengan sangat
mudah.
Berikut ini
adalah satu contoh
penyelesaian masalah Jaringan
kerja
PT. ABC sedang mengembangkan seperangkat meja-kursi,
proyek ini memerlukan sepuluh kegiatan. Beberapa kegiatan tergantung pada
penyelesaian kegiatan sebelumnya. Masing-masing kiegiatan memiliki tiga
alternative waktu penyelesaian, yaitu optimis, mungkin, dan pesimis. Data
kegiatan dapat dilihat pada tabel dan gambar berikut:
No
|
Kegiatan
|
Pendahulu
|
Optimis
|
Mungkin
|
Pesimis
|
1
|
A
|
-
|
0,5
|
1,0
|
1,5
|
2
|
B
|
A
|
2,0
|
4,0
|
6,0
|
3
|
C
|
A
|
3,0
|
5,0
|
7,0
|
4
|
D
|
B
|
2,0
|
3,0
|
4,0
|
5
|
E
|
B
|
0,5
|
1,5
|
2,5
|
6
|
F
|
C
|
0,5
|
1,5
|
2,5
|
7
|
G
|
C
|
2,0
|
3,5
|
5,0
|
8
|
H
|
D,F
|
2,0
|
2,5
|
3,0
|
9
|
I
|
E
|
0,5
|
1,0
|
1,5
|
10
|
J
|
G,H,I
|
2,0
|
4,0
|
6,0
|
Tentukan kemungkinan
penyelesaian kegiatan yang termasuk ke dalam jalur kritis !!
Penyelesaiannya adalah sebagai
berikut :
1. Pilih Modul PERT/CPM,
lalu pilih ,menu file, New Problem , Lalu pilih type Probabilistic PERT
a.
Pada bagian Problem title diisi dengan Masalah PERT.
b.
Pada kolom Number of Activities diisi dengan 10.
c.
Pada kolom Time Unit diisi dengan Week.
2.
klik ok
sehingga muncul tampilan untuk menginput data masalah PERT seperti berikut ini :
2.
Masukkan data pada tabel diatas , gunakan titik untuk
menuliskan angka pecahan, sedangkan untuk pemisah kegiatan pendahulu gunakan
koma ( misal G, H,I ).
3. kemudian simpan di folder
D:\data\namamu ( dengan klik menu File,
Save problem).
Dengan nama lat_pert.
4.
Klik Menu File, Load problem, lalu pilihlan
lat_pert.cpm
5.
klik menu Solve
and Analyze, lalu pilih Solve the
Problem, maka akan muncul hasilnya seperti berikut :
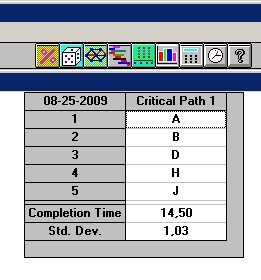
Dari tampilan tersebut diketahui bahwa
untuk menyelesaikan proyek adalah 14,5 minggu dan terdapat 1 jalur kritis.
Untuk menampilkan solusi dalam bentuk grafik, klik menu Result, Show critical Path.
Untuk menampilkan Jalur kritis dalam
bentuk diagram klik menu Result, Grapich
Activity Analysis.
Untuk menampilkan Jalur kritis dalam
bentuk diagram gantt klik menu Result,
Gantt Chart .
6. Untuk menghitung probalitas penyelesaian proyek klik
menu Result, Perform Probality Analysis.
Anda perlu mengisi perkiraan penyelesaian proyek pada isisan B Desired completion time in week dengan angka perkiraan anda, untuk contoh kita
isi dengan waktu normal proyek yaitu 14,5 minggu. Lalu klik Compute Probality .
Hasilnya adalah kemungkinan penyelesaian
kegiatan yang termasuk jalur kritis dalah 0,50 atau 50%. ( apabila angka ini lebih kecil dari 26%
berarti masih banyak sumber daya yang belum dimanfaatkan dan bila angka lebih
dari 64% maka terlalu banyak sumber daya yang digunakan. ).
C. Analisa Biaya
Contoh kasus :
Melanjutkan soal diatas jika anggaran yang disediakan
sebesar 80 jt, maka carilah biaya untuk pekerjaan yang diper cepet sesuai
dengan tabel berikut ini !
no
|
kegiatan
|
pendahulu
|
Waktu (minggu)
|
Biaya
|
||
Normal
|
dipercepat
|
normal
|
dipercepat
|
|||
1
|
A
|
1,0
|
0,5
|
5
|
6
|
|
2
|
B
|
A
|
4,0
|
2,0
|
7
|
10
|
3
|
C
|
A
|
3,0
|
4,0
|
10
|
12
|
4
|
D
|
B
|
1,5
|
3,0
|
8
|
8
|
5
|
E
|
B
|
1,5
|
1,5
|
4
|
4
|
6
|
F
|
C
|
1,0
|
1,0
|
4
|
5
|
7
|
G
|
C
|
2,5
|
2,5
|
15
|
20
|
8
|
H
|
D,F
|
2,5
|
2,5
|
6
|
6
|
9
|
I
|
E
|
1,0
|
1,0
|
3
|
3
|
10
|
J
|
G,H,I
|
3,0
|
3,0
|
9
|
10
|
Penyelesaiaanya adalah sebagi berikut :
1.
Pilih Modul PERT/CPM, lalu pilih ,menu file, New Problem , Lalu pilih type Deterministic CPM
a.
Pada bagian Problem title diisi dengan biayapert.
b.
Pada kolom Number of Activities diisi dengan 10.
c.
Pada kolom Time Unit diisi dengan Week.
d.
Pada pilihan Select CPN data Field di pilih normal time, crash time, normal cost
dan crash cost.
2.
klik ok
sehingga muncul tampilan untuk menginput data masalah Network seperti berikut :
3.
Masukkan data pada tabel diatas , gunakan titik untuk
menuliskan angka pecahan, sedangkan untuk pemisah kegiatan pendahulu gunakan
koma ( misal G, H,I ).
kemudian simpan di folder
D:\data\namamu ( dengan klik menu File,
Save problem).
Dengan nama lat_biaya.
4.
Klik Menu File, Load problem, lalu pilihlan
lat_biaya.cpm
5.
klik menu Solve
and Analyze, lalu pilih Solve
Critical Path Using Normal Time, maka akan muncul hasilnya seperti berikut :
Dari tampilan tersebut hasilnya masih sama
yaitu 14,5 minggu karena waktu penyelesaiannya masih normal, sekarang kita akan
coba untuk mempercepat waktu penyelesaian proyek menjadi 11 minggu.
6.
klik Result,
perform Crashing Analysis. Pada
kolom Desired completion time kita isi dengan 11. lalu ok. Maka akan
muncul hasilnya seperti berikut :
Hasilnya bahwa waktu percepatan memerlukan
tambahan biaya 8jt, sehingga total biaya
menjadi 79jt. Kegiatan yang dipercepat terlihat pada kolom suggested time.
Untuk menampilkan dalam bentuk diagram klik menu Result,
PERT/Cost grapihic.
D. PRAKTEK
1. perhatikan
tabel di bawah ini
kegiatan
|
Waktu (hari)
|
Kegiatan pendahulu
|
||
optimis
|
rencana
|
pesimis
|
||
A
|
8
|
10
|
12
|
-
|
B
|
6
|
7
|
9
|
-
|
C
|
3
|
3
|
4
|
-
|
D
|
10
|
20
|
30
|
A
|
E
|
6
|
7
|
8
|
C
|
F
|
9
|
10
|
11
|
B,D,E
|
G
|
6
|
7
|
10
|
B,D,E
|
H
|
14
|
15
|
16
|
F
|
I
|
10
|
11
|
13
|
F
|
J
|
6
|
7
|
8
|
G,H
|
K
|
4
|
7
|
8
|
I,J
|
L
|
1
|
2
|
4
|
G,H
|
a.
hitung probalitas jika proyek akan diselesaikan dalam
70 hari !
b.
hitung probalitas jika proyek akan diselesaikan dalam
80 hari !
2. berikut
ini tabel pelaksanaan proyek pembangunan jembatan
kegiatan
|
Waktu (minggu)
|
Biaya per minggu
|
Biaya percepatan per
minggu
|
||
normal
|
cepat
|
normal
|
cepat
|
||
A
|
2
|
1
|
22000
|
23000
|
1000
|
B
|
3
|
1
|
3000
|
34000
|
2000
|
C
|
2
|
1
|
26000
|
27000
|
1000
|
D
|
4
|
3
|
48000
|
49000
|
1000
|
E
|
4
|
2
|
56000
|
58000
|
1000
|
F
|
3
|
2
|
30000
|
30500
|
200
|
G
|
5
|
2
|
80000
|
86000
|
2000
|
H
|
2
|
1
|
16000
|
19000
|
3000
|
Apakah proyek tersebut dapat dipercepat 2 minggu ?
Apa pengaruhnya terhadap biaya proyek ?
MODUL VIII
TEORI ANTRIAN
A. MAKSUD DAN TUJUAN
1.
Tujuan
Menyelesaikan masalah antrian
pada Riset Operasi dengan menggunakan metode QA agar optimal.
2.
Maksud
Agar mahasiswa mampu menyelesaikan masalah antrian. dengan
menggunakan WINQSB
B. TEORI
Dengan menggunakan
modul Queing Analysis pada
WINQSB, anda dapat menyelesaikan suatu masalah
antrian dengan sangat mudah.
Berikut ini
adalah satu contoh
penyelesaian masalah antrian
PT. ABC memiliki system layanan pelanggan melalui
telpon dan dilayanai oleh seorang petugas, menurut catatan, rata-rata tiap
menit ada tiga telpon dari pelanggan ( biasa dinyatakan dengan λ atau lamda) dan masing-masing memerlukan 15 detik untuk mendapat solusi ( biasa dinyatakan µ atau myu). Jumlah
penelpon yang menunggu tidak dibatasi, karena sementara dapat dilayani oleh
computer dan mesin penjawab otomatis.
Gaji seorang
operator adalah Rp 20 per menit. Biaya seorang penelpon adalah Rp 50 per menit
( baik dijawab oleh operator maupun mesin penjawab ).
Perusahaan
ingi mengetahui apakah perlu menambah operator atau tidak , bahkan manager
ingin mengetahui berapakah jumlah operator yang optimal untuk kondisi sekarang
ini.
Penyelesaiannya adalah sebagai berikut :
1.
Pilih Queuing
Analysis, lalu pilih ,menu file, New Problem , Lalu pilih type Simple M/M System.
a.
Pada bagian Problem title diisi dengan Masalah Antrian.
b.
Pada kolom Time unit diisi dengan Menit.
c.
Pada option Entry Format pilih Simple M/M System.
2.
klik ok
sehingga muncul tampilan untuk menginput data masalah Antrian seperti berikut ini :
3.
Inputkan data yang ada pada table diatas,
. Item service rate diisi 4, karena
menurut soal setiap pelanggan butuh waktu 15 detik, dengan kata lain dlm 1
menit ada 4 pelanggan nyang masalahnya terselesaikan.
. Item ustomer arrival rate diis3 ,
karena ada 3 penelpon yang menelpon dalam 1 menit.
. Item busy server cost permenit adalah
Rp 20 atau sama dengan gaji seorang operator, demikian juga Idle server
permenit Rp 20 karena tidak menjawab telpon pegawai tetap di gaji.
.Item Customer waiting cost per menit
adalah Rp 50, baik ketika sedang dijawab oleh operator ataupun mesin p-enjawab,
sehingga item Customer beingserved per menit juga diisi Rp 50. kemudian simpan
di folder D:\data\namamu\ ( dengan klik menu File, Save problem).
Dengan nama lat_antri
4.
Klik Menu File, Load problem, lalu pilihlan
lat_antri.QAA
5.
klik menu Solve
and Analyze, lalu pilih Solve the
Performance, maka akan muncul hasilnya seperti berikut :
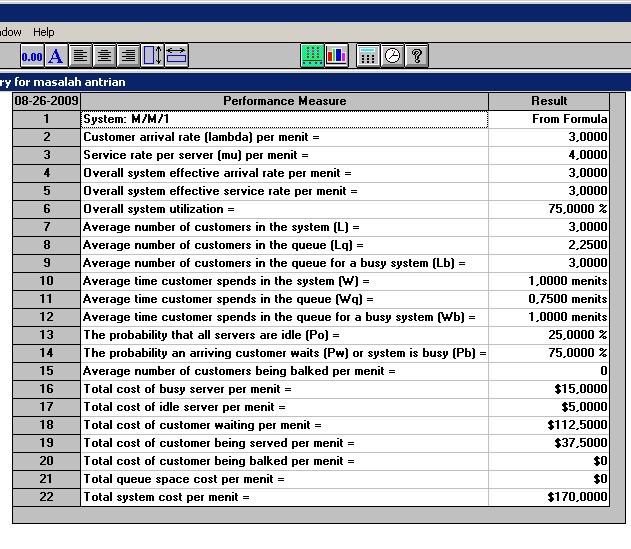
Dari tampilan tersebut diketahui bahwa :
a.
Biaya total per menit tersebut adalah Rp 170
b.
Diketahui λ=3 , µ= 4 ( 4 orang per menit)
c.
L ( baris 7,banyaknya pelanggan yang diulayani dan
dalam antrian )
λ
= µ(µ−λ)
i. =  = 3
= 3
d.
Lq ( baris 8, banyaknya pelanggan dalam antrian ) = λ
2
= 32 =2,25
µ(µ−λ) 4(4−3)
e.
W ( baris 10, rata-rata pelanggan menghabiskan waktu
dalam antrian dan ketika dilayani
1 
= =
=1 menit
µ−λ
f.
Wq (baris 11, rata-rata waktu pelanggan menunggu
dilayani ) =
λ

= =
0,75 menit atau 45 detik.
µ(µ−λ)
λ 
g.
Po (baris 13, kemungkinan system menganggur ) = 1- =
1- = 25 %
µ
h.
Pw (baris 14, kemungkinan pelanggan harus menunggu )
atau Pb ( kemungkinan system λ 3 sibuk ) = = = 75 %.
µ
4
Analisa tambahan layanan
1. Klik
menu window pilih anhka 1 untuk kembali ke menu sebelumnya.
2. Ubah
Numbe Of Server dari 1 menjadi 2.
3. Jalan
kan menu solve and analyze, lalu pilih solve the performance. Maka akan muncul
tampilan seperti berikut :
Hasil diatas menunjukkan perbaikan
rata-rata waktu tunggu oleh pelanggan, demikian juga dengan biaya total system
juga turun dari Rp 170 menjadi Rp 83,6364.
Langkah selanjutnya kita analisa lagi jika titik layanan di
tambah 1 ( sehinggamenjadi 3),
1. ulangi
langkah 1.
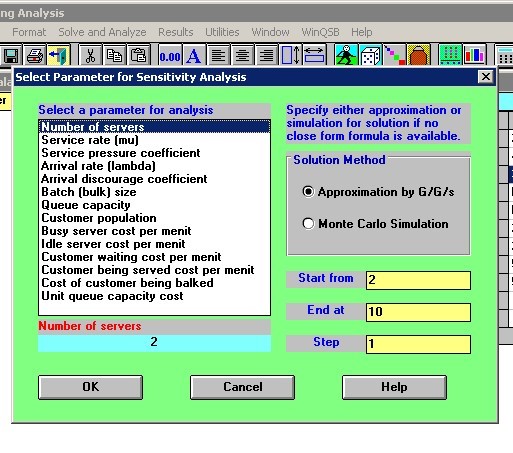
2. Jalan
kan menu solve and analyze, perform
Sensitivy Analysis, sehingga tampilah sebagai berikut:
6. Pada
isian start from isikan dengan angka 1 dan pada isian end
at isikan dengan 5, pada isian step isikan 1 . lalu
klik ok. Maka akan muncul tampilan
sebagai berikut :
Perhatikan pada kolom
paling kanan ( total cost ). Biaya yang paling sedikit ada di baris kedua yaitu
Rp 83,6364. dengan demikian dari berbagai pilihan ( 1 hingga 5 operator ) yang
paling hemat sekaligus memiliki kinerja yang baik adalah 2 operator.
1. untuk
menampilkan analisa dalam bentuk grafik klik, result, sensitivity
analysis-graph.
C. PRAKTEK
1.Sebuah toko memiliki 300 pelanggan yang dating
setiap sabtu, pihak manajemen ingin menentukan berapa banyak kasir yang harus
ditugasi pada hari sabtu, seorang kasir di gaji Rp 8 (dalam ribuan) perjam.
Bila hanya ada 1 kasir waktu tunggu masing-masing pelanggan sekitar 10 menit.
Bila ada 2 kasir yang bertugas, waktu tunggu menjadi 6 menit, bila ada 3 kasir
waktu tunggu menjadi 4 menit dan bila ada 4 kasir waktu tunggu menjadi 3 menit
.
Berdasarkan survey, pihak toko mengalami
kerugian Rp 10 (x 100) per jam dari hilangnya kesempatan penjualan sekaligus
nama baik toko juga dirugikan.
Hitunglah berapa jumlah kasir yang optima
untuk menekan biaya, tetapi toko dapat memberikan pelayanan yang terbaik !!
2.Sebuah SBPU ingin meningkatkan layanan kepada
pelanggan. Saat ini, kondisi di SPBU pada jam-jam sibuk jumlah kendaraan yang
datang 50 mobil per jam. Tingkat kedatangan mobil mengikuti pola distribusi
Poisson. Setiap mobil akan dilayani rata-rata 1 menit dengan distribusi
Eksponensial. Hitunglah :
a.
Tingak kesibukan karyawan bagian penjualan.
b. Jumlah
rata-rata dalam antrian .
c.
Jumlah rata-rata antrian dalam sistem.
d. Waktu
menunggu rata-rata dalam antrian.
e.
waktu menuggu rata-rata dalam system.
f. Besarnya
probalitas lebih dari 1 mobil dalam system dan lebih besar dari 4 mobil dalam
sistem.
MODUL IX
TEORI PERSEDIAAN
A. MAKSUD DAN TUJUAN
1.
Tujuan
Menyelesaikan masalah antrian
pada Riset Operasi dengan
menggunakan metode Inventory Theory and System agar
optimal.
2.
Maksud
Agar mahasiswa mampu menyelesaikan masalah persediaan. dengan menggunakan WINQSB
B. TEORI
Dengan menggunakan
modul Inventory Theory and System pada WINQSB, anda
dapat menyelesaikan suatu masalah persediaan dengan sangat mudah.
Berikut ini adalah
satu contoh penyelesaian
masalah persediaan:
PT ABC menghadapi masalah dengan pengadaan kayu yang kan digunakan
sebagai bahan produksi. Kebutuhan kayu untuk pembuatan kursi selam 1 tahun
adalah 3.600 lembar. Biaya melakukan sekali pemesanan adalah RP 200. biaya
simpan perlembar kayu adalah Rp 25 per tahun, harga per lembar kayu adalah Rp
100.
Perusahaan ingin mengetahui berapa kali
harus memesan kayu untuk memenuhi kebutuhan selama setahun, atau berapa banyak
kayu harus dipesan setiap kali pemesanan, agar biaya yang di keluarkan minimal.
Penyelesaiannya adalah sebagai berikut :
1.
Pilih modul Inventory
Theory and System, lalu pilih ,menu file, New Problem , Lalu pilih type Deterministic Demand economic Order
Quantity (EQQ) Problem.
a.
Pada bagian Problem title diisi dengan Masalah persediaan.
b.
Pada kolom Time unit diisi dengan Tahun.
2.
klik ok
sehingga muncul tampilan untuk menginput data masalah Persediaan seperti berikut ini :
3.
Inputkan data yang ada pada soal diatas, isikan 3600 pada deman per year, isikan 200
pada order setup cost per order, isikan 25 pada unit holding cost per year, dan
100 pada unit acquisition cost without discount.
kemudian simpan di folder
D:\data\namamu\ ( dengan klik menu File,
Save problem).
Dengan nama lat_inven
4.
Klik Menu File, Load problem, lalu pilihlan
lat_inven.ITS
5 Klik menu Solve and
Analyze, lalu pilih Solve the
Problem, maka akan muncul
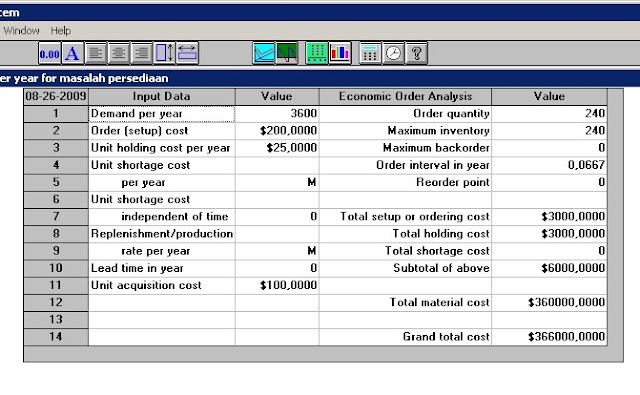 Dari tampilan diatas terlihat bahwa seriap kali
pemesanan jumlahnya adalah 240 lembar kayu. Karena kebutuhan per tahun adalah
3600 lembar, berarti harus ada pemesanan sebanyak 3600/240 = 15 x. total biaya
yang harus dikeluarkan adalah Rp 360.000. 6. Bila ingin menampilkan grafik biaya,
pilih menu Result, Graphic Cost
Analysis.
Dari tampilan diatas terlihat bahwa seriap kali
pemesanan jumlahnya adalah 240 lembar kayu. Karena kebutuhan per tahun adalah
3600 lembar, berarti harus ada pemesanan sebanyak 3600/240 = 15 x. total biaya
yang harus dikeluarkan adalah Rp 360.000. 6. Bila ingin menampilkan grafik biaya,
pilih menu Result, Graphic Cost
Analysis.
C. FIXED ORDER QUANTITY
contoh
soal untuk kasus yang lebih rumit.
PT ABC menghadapi masalah dengan
pengadaan kayu yang kan digunakan sebagai bahan produksi. Kebutuhan kayu untuk
pembuatan kursi selam 1 tahun adalah 3.600 lembar. Biaya melakukan sekali
pemesanan adalah RP 200. biaya simpan perlembar kayu adalah Rp 25 per tahun,
harga per lembar kayu adalah Rp 100.
PT ABC memiliki permintaan yang acak dan setiap kekurangan persediaan
dilakukan pemesanan dengan biaya Rp 20, waktu pengantaran hamper dipastikan 20
hari ( 20 / 360= 0,0555).
Penyelesaiannya adalah sebagai berikut :
1.
Pilih modul Inventory
Theory and System, lalu pilih ,menu file, New Problem , Lalu pilih type Continous Review Fixed-Order-Quantity (s,
Q) system.
a.
Pada bagian Problem title diisi dengan Masalah persediaan lanjut .
b.
Pada kolom Time unit diisi dengan Tahun.
2.
klik ok
sehingga muncul tampilan untuk menginput data masalah Persediaan seperti
berikut ini :
3. Inputkan data yang ada pada soal diatas, isikan 3600 pada deman distribution,isikan 50 pada standar deviation isikan 200 pada order setup cost per order, isikan 100 pd unic acquisition cost, isikan 25 pada unit
holding cost per year, dan 100 pada estimed % of shortage, isikan 20 pada unit
backorder cost, isikan 0.0555 pada constant value.
kemudian simpan di folder
D:\data\namamu\ ( dengan klik menu File,
Save problem).
Dengan nama lat_inven2
4. Klik Menu File, Load problem, lalu pilihlan
lat_inven2.ITS
5
Klik menu Solve
and Analyze, lalu pilih Solve the
Problem, maka akan muncul
6 . klik solve maka akan muncul tampilan :
Dari tampilan diatas terlihat bahwa
sebaiknya perusahaan segera memesan persediaan pada saat persediaan mencapai
jumlah 215,9491. jumlah unit yang dipesan setiap kali memesan adalah 245,3235
unit, jumlah persediaan minimum adalh 16, 1491 unit.
Biaya total yang harus dibayar adalah Rp 360.000 pertahun.
7. untuk
membuat grafik yang menggambarkan kebutuhan pesediaan selama 1 tahun, klik menu
Result, graphic Inventory Profile.
D. PRAKTEK
1. permintaan sabun dalam 1 tahun
adalah 10.000 biji, biaya untuk pemesanan adalah Rp 10, biaya angkut untuk
setiap 100 sabun adalah Rp1. permintaan sabun dlm setahun relative
stabil.
a.
Berapa jumlah sabun yang harus dipesan untuk
meminimumkan biaya?
b. berapa
kali harus dilakukan pemesanan dlam 1 tahun dan berpa jumlah biaya pemesanan
dlm 1 tahun?
c.
berapa rata-rata persediaan selama 1 tahun dan berapa
besar biaya penyimpanan dlm 1 tahun?
2.. sebuah
toko ingin membeli mie instant untuk persediaan. Permintaan tiap tahun untuk
mie instant adalah 4.000 karton. Harga tiap karton adalah Rp 90. biaya pengdaan
adalah 10 % dari tiap karton. Biaya yang harus dibayar untuk setiap kali
pemesanan adalah Rp 25. waktu tunggu sejak memesan sampai mie dating adalah 2
minggu. Permintaan per minggu menunggu adalah 80 karton.
a.
Hitung persediaan optimasinya.
b. berapa
titik pemesanan kembali?
c.
Berapa rata-rata persediaan dan berapa besar biaya
simpan per tahun ?
d. berapa
kali sebaiknya toko memesan mie dalam setahun dan berapa biaya pemesanan dalam
1 tahun?
MODUL X
PERAMALAN
A. MAKSUD DAN TUJUAN
1.
Tujuan
Menyelesaikan masalah peramalan
pada Riset Operasi dengan menggunakan metode
Forecasting agar optimal.
2.
Maksud
Agar
siswa mampu menyelesaikan masalah
peramalan. dengan menggunakan WINQSB
B. TEORI
Dengan menggunakan
modul Forecasting pada WINQSB,
anda dapat menyelesaikan suatu
masalah persediaan dengan sangat mudah.
Berikut ini adalah
satu contoh penyelesaian
masalah peramalan:
PT ABC ingin memperkirakan permintaan produknya berdasarkan
pendapatan keluarga. Perusahaan melakukan survey terhadap 10 pelanggan secara
acak. Permintaan produk dinyatak dalam rupiah. Datanya dapat dibawah ini:
no
|
permintaan
|
Pendapatan
|
Masa keja (thn)
|
1
|
100
|
20000
|
2
|
2
|
130
|
30000
|
2
|
3
|
200
|
100000
|
5
|
4
|
140
|
40000
|
4
|
5
|
170
|
70000
|
5
|
6
|
120
|
20000
|
3
|
7
|
220
|
130000
|
6
|
8
|
150
|
50000
|
4
|
9
|
160
|
55000
|
3
|
10
|
190
|
80000
|
4
|
Penyelesaiannya adalah sebagai berikut :
1.
Pilih modul Forecasting
and Linar Regression lalu pilih ,menu file, New Problem , Lalu pilih type Linear Regression.
a.
Pada bagian Problem title diisi dengan Masalah peramalan.
b.
Pada kolom number of factor diisi dengan 3.
c.
Pada kolom Number of observations diisi dengan 10.
2.
klik ok
sehingga muncul tampilan untuk menginput data masalah Peramalan seperti berikut
ini :
3.
Ubahlah nam variable atau judul kolom, dengan meng klik
menu Edit, Factor (variable) Names, lalu gantilah factor1 dengan permintaan ,
factor 2 dengan pendapatan dan factor 3
dengan Masa kerja, jika sudah selesai klik OK.
4.
Inputkan data yang ada pada tabel diatas.
kemudian
simpan di folder D:\data\namamu\ ( dengan klik menu File, Save problem).
Dengan nama lat_ramal
5.
Klik Menu File, Load problem, lalu pilihlan
lat_ramal.FCC
6. Klik
menu Solve and Analyze, lalu pilih Perform Linear Regression, maka akan
muncul .
Klik ok maka akan tampil :
Dari tampilan diatas terlihat bahwa nilai adusted R2-nya
0,9402 (94,02%) yang berarti modelnya sudah cukup baik. Niali sttistik t
yang lebihbesr daei 2hanya kons-tanta (8,748) dan variable pendapatan (5,556)
yang berarti signifikan. Sedang variable masa kerja tidak signifikan karena
nilai t-nya hanya 0,195.
Bila digunakan untuk peramalan model diatas akan menjadi
seperti berikut ni:
Permintaan = 95,337 + 0,099 pendpatan + 0,951
masa kerja
Nilai t ( 8,748) (5,556) (0,195)
Anda dapat menampilkan persamaan
diatas dengan menjalankan menu Result, show
regression equation.
7.
untuk menampilkan tabel ANOVA , aklik Menu Result, show ANOVA
8.
Bila ingin menampilkan garis regresi pilih menu Result, Show regression line.
C. PERKIRAAN DENGAN ANALISA REGRESI
Perusahaan ingi melakukan prediksi permintaan produk terhadap pelanggan
yang pendapatannya Rp 45000 dan masa kerjanya 2 tahun.. untuk melakukan hal itu
langkahlangkahnya dalah :
1.
klik windows pilih 1 untuk kembali ke menu input data.
2.
klik solve and analyze, Perform estimation and
prediction, maka akan muncul tampilan :
3.
klik enter value for independent variable dan
masukkan angka yang dipredikasi yaitu
45000 pada variable pendapatan dan 2
pada masa kerja, lalu klik ok.
4.
klik ok sekali lagi, kemudian akan tampilhasilnya
sebagai berikut :
Tampilan diatas menunjukkan permintaan produk oleh
keluarga dengan penghasilan Rp 45000 dan masa kerja 2 tahun adalah Rp 141,989 (
abaikan variable masa kerja yang tidak signifikan).
C. PERAMALAN DENGAN TIME SERIES
PT ABC ingin memperkirakan
permintaan produknya pada bulan ke-6 berdasarkan data pendapatan keluarga
selama 5 bulan. Peusahaan sudah melakukan survey terhadap 10 pelanggan secara
acak. Permintan produk dinyatak dalam rupiah. Datanya dapat dilihat pada tabel
berikut :
no
|
permintaan
|
Pendapatan
|
Masa keja (thn)
|
1
|
100
|
20000
|
2
|
2
|
130
|
30000
|
2
|
3
|
200
|
100000
|
5
|
4
|
140
|
40000
|
4
|
5
|
170
|
70000
|
5
|
6
|
120
|
20000
|
3
|
7
|
220
|
130000
|
6
|
8
|
150
|
50000
|
4
|
9
|
160
|
55000
|
3
|
10
|
190
|
80000
|
4
|
Penyelesaiannya dalah sebagai
berikut :
1. Pilih
modul Forecasting and Linar Regression
lalu pilih ,menu file, New Problem , Lalu pilih type Time series Forecasting.
a. Pada bagian Problem title diisi dengan Masalah peramalan2.
b.Pada kolom number of time unit dengan bulan.
c. Pada kolom Number of time unit diisi dengan 5.
2. klik
ok sehingga muncul tampilan untuk
menginput data masalah Peramalan seperti berikut ini :
3. Inputkan
data yang ada pada tabel diatas.
4. kemudian
simpan di folder D:\data\namamu\ ( dengan klik menu File, Save problem).
Dengan nama lat_ramal2
5. Klik
Menu File, Load problem, lalu pilihlan
lat_ramal2.FCC
6. Klik
menu Solve and Analyze, lalu pilih Perform forecasting, maka akan muncul
Pilih simple average, pada kolom
number of periods to forecast isikan dengan 1, lalu klik ok, maka hasilnya sebagai berikut :
Dari tampilan di atas dapat
diketahui bahwa prediksi permintaan produk pada bulan ke-6 adalah sebesar Rp
148.
Untuk menapilkan peramalan dalam
bentuk grafik klik menu result, show forecasting in graph.
E. PRAKTEK
1.Sebuah
perusahaan jasa pemandu wisatawan memiliki data kedatangan wisatawan sebagai
berikut :
bulan
|
Jumlah wisatawan
|
Pengunjung candi
|
1
|
7
|
15
|
2
|
2
|
10
|
3
|
6
|
13
|
4
|
4
|
15
|
5
|
14
|
25
|
6
|
15
|
27
|
7
|
16
|
24
|
8
|
12
|
20
|
9
|
14
|
27
|
10
|
20
|
44
|
11
|
15
|
34
|
12
|
7
|
17
|
a. Gambarkan
data tersebut ke dalam grafik, untuk mengetahui apakah modelnya bersifat
linear.
b. Carilah
persamaan Regresinya
c. Berapa
banyak wisatawan yang mengunjungi candi bila jumlah wisaatawan yang adatang
1000?
d. Berapa
pengunjung candi bila tidak ada wisatawan
datang.
2.Seorang
dosen memiliki data nilai UTS dan UAS 10 orang mahsiswa, seperti pada tabel
berikut:
mahasiswa
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Nilai UTS
|
95
|
74
|
89
|
82
|
84
|
69
|
72
|
98
|
87
|
90
|
Nilai UAS
|
90
|
80
|
83
|
84
|
87
|
73
|
78
|
95
|
90
|
84
|
a.
Carilah persamaan regresi yang dapat igunakan untuk
memprediksi nialai UAS berdasarkannilai UTS seorang mahasiswa
b.
Perkirakan seorang mahasiswa mendapat nilai UTS 82,
berapakah nilai UAS ny? Demikian juga mahasiswa yang nilai UTS nya 90?
--- End of modul ----